Cien años de la teoría general de la relatividad
Sergio de Régules
Foto: F. Schmutzer/PD
Einstein la describió como “la idea más afortunada” de su vida, pero convertirla en una teoría completa le llevó al físico años de esfuerzo y de pasar constantemente del éxtasis a la zozobra. La última etapa del proceso fue también el mes más intenso y productivo de la carrera de Einstein.
La fuerza de gravedad siempre fue la rara de la familia. Cualquier otro empujón o jalón se siente físicamente: nos vamos de bruces cuando el coche da un frenazo. Nos aplastamos contra el respaldo del asiento cuando arranca de golpe. En las curvas el cuerpo se nos va de lado en el sentido opuesto. Cuando nos chocan por detrás, se nos tuerce el cuello por la inercia de la cabeza (la inercia es la resistencia de un objeto a cambiar de movimiento). El cuerpo humano abandonado a estas fuerzas se reduce a un vil objeto físico con masa e inercia. Pero abandónense ustedes a la pura fuerza de gravedad, sin soporte de suelo ni silla, y verán por qué es la rara de la familia. No necesitan tirarse de lo alto de un edificio. Basta subirse a uno de esos juegos de feria que te ponen en caída libre momentáneamente. Me consta porque una vez me dejé convencer por mi hija de subirme con ella a uno de esos juegos. Lo más notable durante la caída libre fue la sensación de que me flotaban los brazos y mis posaderas dejaban de ejercer presión sobre el asiento: cayendo por efecto de la gravedad era como si la gravedad hubiera desaparecido.
Caída libre
En su libro Vida de Galileo, Vincenzo Viviani, último alumno y primer biógrafo del científico italiano, cuenta que su maestro desmintió a Aristóteles en lo tocante a la caída libre “con repetidos experimentos hechos desde lo alto del campanario de Pisa con participación de los otros maestros y filósofos”. Esta frase es la base de la leyenda de que Galileo dejaba caer bolas de plomo y de madera desde lo alto de la torre de Pisa ante la mirada atónita y furibunda de sus detractores aristotélicos. La leyenda seguramente es falsa, pero no hay duda de que Galileo sabía que dos cuerpos de pesos distintos caen exactamente al mismo tiempo si no hay resistencia del aire. Aquí se puede ver una dramática demostración con plumas y bolas de boliche: www.youtube.com/ watch?v=E43-CfukEgs.
Unos años después de Galileo, Isaac Newton lo explicó así: en virtud de la masa, la gravedad tira con más fuerza de la bola de boliche que de las plumas. Más fuerza debería corresponder a más aceleración, pero, también en virtud de la masa, la bola de boliche tiene más inercia y resiste más tercamente a las aceleraciones que las plumas. Los efectos de jalón gravitacional y resistencia inercial se equilibran exactamente y bola y plumas caen con la misma aceleración. Lo cual no explica nada, sólo cambia un misterio por otro: ¿por qué se equilibran la gravedad y la inercia, dos propiedades en principio completamente distintas? Newton lo consideraba una simple coincidencia.
Idea feliz
Sentado en su taburete de técnico de tercera clase en la oficina de patentes de Berna, Suiza, Albert Einstein, de 28 años, ponderaba el enigma de la caída libre. Dos años antes, en 1905, había publicado tres artículos que llegarían a considerarse revolucionarios, pero el mundo de la investigación científica aún no se decidía a adoptar al joven creador de la teoría especial de la relatividad. El empleo de técnico de tercera clase se lo había conseguido el padre de su amigo y compañero de estudios Marcel Grossmann cuando ninguna universidad quiso contratarlo al salir de la carrera de física. El trabajo era aburrido, pero a Einstein le sobraba tiempo para pensar.
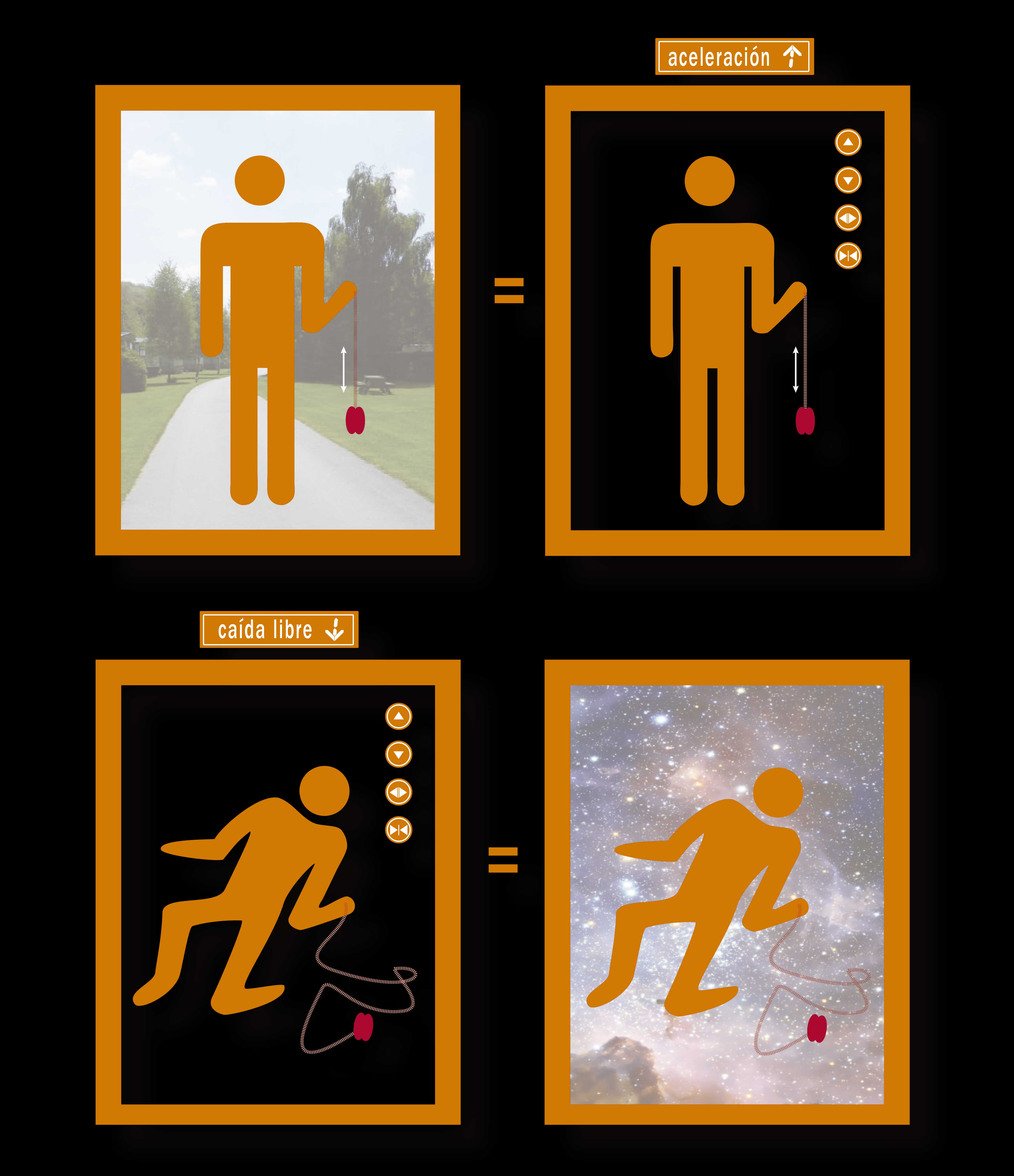
En 1907, pensando en la caída libre, decidió que la coincidencia numérica de la gravedad y la inercia era demasiada casualidad. Si éstas se compensan tan exactamente, tiene que ser porque, en el fondo, son lo mismo. Esto explicaría el misterio de la aceleración en caída libre igual de bien que la simple coincidencia numérica de Newton, pero tendría otras consecuencias. Para entenderlas, Einstein se imagina un elevador sin ventanas. El cable que lo sostiene se rompe y el elevador se desploma. Desde el punto de vista de un observador en tierra, todos los objetos que se encuentran en el elevador caen con la misma aceleración sin importar sus pesos. Pero, ¿qué ven los ocupantes (cuando se les pasa el susto)? Pues lo mismo que yo en mi juego de feria: que todo empieza a flotar, exactamente como si el elevador se encontrara en el espacio, lejos de todo y sin gravedad. Ahora bien, antes de romperse el cable la gravedad mantiene las cosas pegadas al piso; pero esto sería exactamente lo que observarían los ocupantes si en vez de estar en la Tierra, el elevador se encontrara en el espacio y un cohete lo remolcara hacia arriba impartiéndole una aceleración constante.
En resumen, si los ocupantes observan que las cosas flotan dentro del elevador, puede ser que el aparato esté flotando en el espacio o en caída libre en un campo gravitacional. Si los objetos se sienten atraídos hacia el piso, no se puede saber si el aparato está en reposo en un campo gravitacional o acelerándose en el espacio. No hay experimento físico posible que les pueda decir a los ocupantes, en el primer caso, si caen o flotan, en el segundo, si aceleran o gravitan. Las situaciones son equivalentes y por lo tanto indistinguibles. Einstein llamó principio de equivalencia a esta imposibilidad de distinguir entre inercia y gravitación. Años después dijo: “Fue la idea más afortunada de mi vida”. También fue la que más lo hizo batallar.
Einstein style
Hasta aquí no parece que nos hayamos apartado mucho de la idea original de Newton; muy bien: no hay coincidencia, sino equivalencia —podríamos pensar—, ¿y qué? Durante cuatro años Einstein estuvo ocupado con otros asuntos profesionales y personales (véase ¿Cómo ves?, No. 78), pero en 1911, por fin con un puesto académico en una universidad, volvió a pensar en la gravedad y en el elevador y sus ocupantes.
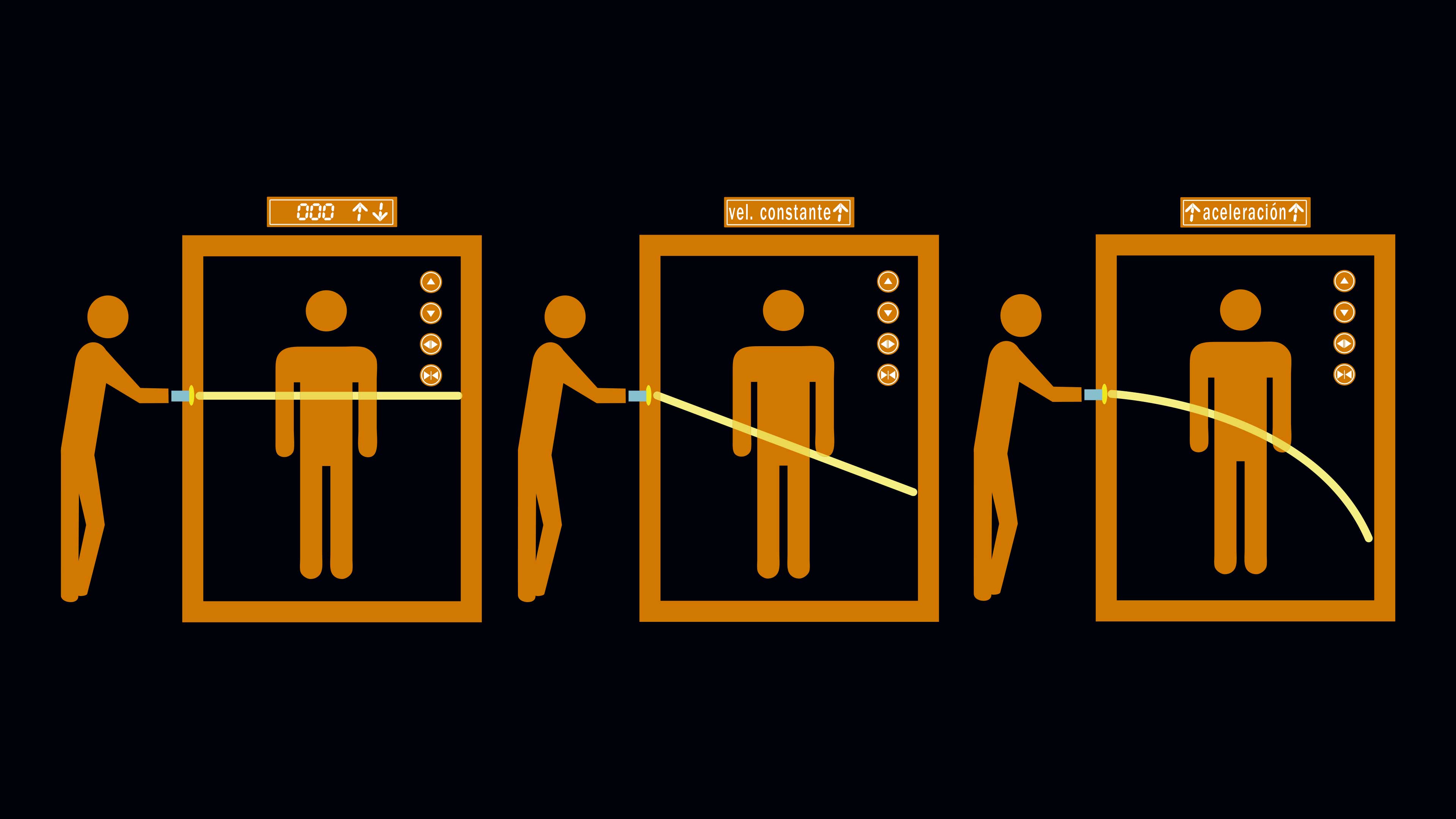
Ahora un rayo de luz entra por un agujerito en la pared. Si el elevador está flotando en el espacio, el rayo atraviesa la cabina en línea recta; por lo tanto, también la cruza en línea recta si el aparato está en caída libre porque las dos situaciones son equivalentes. Pero si el elevador va acelerando, entonces, conforme el rayo de luz avanza por la cabina, ésta va aumentando de velocidad. La luz se va quedando atrás cada vez más rápido y el rayo parece curvarse en el interior del ascensor acelerado. Por el principio de equivalencia, lo mismo tendría que suceder si el elevador estuviera en un campo gravitacional. Conclusión tremenda: la gravedad desvía la luz. He aquí una predicción completamente ajena a la física de Newton, en la que la gravedad sólo afecta a los objetos materiales y la luz siempre viaja en línea recta.
Típico del estilo de Einstein. El personaje tiene fama de genio creador de teorías aparatosas e incomprensibles, pero esta fama es tan falsa como el experimento de la torre de Pisa. Pregúntenle a un físico y les dirá que el estilo de Einstein se caracteriza, al contrario, por su sencillez y elegancia. La genialidad estaría más bien en su capacidad de tomar ideas simples y extraerles consecuencias tremendas por medio de razonamientos intuitivos, incluso antes de construir una maquinaria matemática adecuada.
Es más, Einstein menospreciaba un poco las matemáticas puras y en la universidad no había tenido empacho en volarse las clases de las materias más abstractas, que él consideraba inútiles juegos mentales... de lo que habría de arrepentirse. La primera vez fue en 1909, cuando su antiguo profesor Hermann Minkowski, que otrora lo considerara un holgazán, reformuló la teoría especial de la relatividad de su exalumno de una manera mucho más natural y elegante, en términos de un espacio matemático de cuatro dimensiones al que llamó “espacio-tiempo”. Se podría decir que Einstein expresó las ideas en lenguaje llano y Minkowski las convirtió en poesía. Llegada la ocasión, el ex discípulo tuvo la gallardía de reconocer la aportación de su maestro.
Con su característico poder de intuición, Einstein le sacó mucho jugo al principio de equivalencia entre 1907 y 1911. Otra conclusión basada en éste y en su teoría especial de la relatividad de 1905 es que el tiempo transcurre más lentamente mientras más intensa es la gravedad. Tanto la desviación de la luz como la dilatación del tiempo en un campo gravitacional podían ponerse a prueba, pero no sucedió inmediatamente.
Gravedad es geometría
Con estos resultados, Einstein por fin se decidió a edificar la descripción matemática completa de la equivalencia entre inercia y gravitación. Ya sabemos que ésta implica que el movimiento de los objetos en un campo gravitacional no depende de sus masas: las plumas y las bolas de boliche se mueven exactamente igual. Es más, la trayectoria no depende de ninguna propiedad del objeto, de modo que podríamos considerarla más bien una propiedad del espacio mismo (o, mejor dicho, del espacio-tiempo). Es como si la gravedad moldeara el espacio-tiempo y los objetos sólo se dejaran llevar por sus contornos y altibajos. El principio de equivalencia le exigía a Einstein convertir el campo gravitacional en una especie de paisaje ondulado por el que se deslizan con abandono los cuerpos y la luz. Gravedad es topografía.
Construir la nueva teoría de la gravedad equivalía a establecer ecuaciones que incorporaran la reciprocidad implícita en el principio de equivalencia. Así la expresó años después el físico John Wheeler: la materia le dice al espacio cómo deformarse, el espacio le dice a la materia cómo moverse.
Einstein no tardó en darse cuenta de que en esta tarea no se podía usar la geometría usual, en la que el camino más corto entre dos puntos es una línea recta y las rectas paralelas nunca se cruzan. Lamentablemente, desconocía las matemáticas necesarias. Ni siquiera estaba enterado de que ya existían. Uno se puede imaginar a sus antiguos profesores meneando un dedo al tiempo que sentencian: “¡te lo dijimos!”
“Ayúdame, si no me vuelvo loco”, le escribió Einstein a su viejo amigo Marcel Grossmann, siempre más atento que él en las clases de matemáticas cuando eran estudiantes de física en Suiza. Bajo la tutela de Grossmann, Einstein aprendió la geometría de espacios curvos desarrollada por Carl Friedrich Gauss y Bernhard Riemann en el siglo XIX y el cálculo tensorial de Gregorio Ricci y Tullio Levi-Civita, que sirve para construir ecuaciones que no cambian cuando cambia el sistema de coordenadas. En otras palabras, el cálculo tensorial deja ver lo esencial por encima de los simples puntos de vista, la herramienta ideal para una teoría de la relatividad.
Talacha e insomnio
Einstein y Grossmann colaboraron entre 1912 y 1914. Las matemáticas de espacios curvos eran inimaginablemente engorrosas. Cuando obtenían ecuaciones que satisfacían una de sus exigencias, resultaba que no satisfacían las otras. Había demasiadas posibilidades. En 1913 los colaboradores publicaron un esbozo de la futura teoría general de la relatividad en el que las ecuaciones no salían completamente independientes de las coordenadas, para frustración de Einstein. Luego el obstinado físico siguió trabajando por su cuenta. En sus cartas decía que se afanaba “como un loco” y que el esfuerzo era “sobrehumano”. Al mismo tiempo tenía que sortear considerables problemas personales con su primera esposa, Mileva Maric, de la que se estaba separando y que continuamente le pedía dinero. Además, Einstein había entablado una relación amorosa con su prima, Elsa Löwenthal, y Mileva no quería que se enteraran sus hijos, de 10 y cuatro años. Por si fuera poco Europa se estremecía en la inestabilidad que llevó a la Primera Guerra Mundial. Solitario en su austero departamento de Berlín, Einstein comía mal y dormía peor. Para relajarse tocaba el violín. A fines de junio de 1915 Einstein presentó sus avances en una serie de conferencias en la Universidad de Gotinga, hogar académico del matemático más célebre de Europa, David Hilbert. “Estoy encantado con Hilbert”, escribió Einstein en una carta después de discutir sus cuitas con el matemático. El sentimiento era mutuo. Hilbert quedó muy complacido con Einstein y con la teoría general de la relatividad. Pero ésta era un problema matemático incompleto, y por lo tanto un reto irresistible para cualquier matemático que se respete. Hilbert se integró a la carrera para el sprint final.
En octubre Einstein había caído nuevamente presa de la desesperación: las ecuaciones no se aplicaban bien al movimiento de rotación ni conservaban su forma en cualquier marco de referencia, requisito indispensable para garantizar la relatividad de los movimientos acelerados y con ella el principio de equivalencia. Por si no bastara, tampoco explicaban correctamente el único fenómeno bien conocido que exigía una nueva teoría de la gravedad: las irregularidades del movimiento del planeta Mercurio. Observadas desde el siglo XIX, nadie había podido explicarlas usando la gravitación universal de Newton, y por lo tanto eran un importante patrón contra el que tenía que medirse la teoría general de la relatividad.
Carrera contra reloj
En noviembre de 1915 Einstein se comprometió a dar cuatro conferencias ante la Academia Prusiana. “Durante los últimos cuatro años he tratado de establecer una teoría general de la relatividad”, dijo Einstein al principio de su primera conferencia, lo que daba a entender que no lo había logrado. Ahora Hilbert le pisaba los talones. El matemático le había informado que había un error en su último esbozo, a lo que Einstein, con cierta exasperación, contestó que él también se había dado cuenta. Luego le envió a Hilbert una copia de su primera conferencia.
A partir de ese momento, la carrera de Einstein adquiere un ritmo frenético. El 11 de noviembre presenta nuevas ecuaciones, pero éstas no acaban de resolver todos los problemas. Le manda la conferencia a Hilbert y como quien no quiere la cosa, le pregunta cómo va él. El matemático le contesta que ha encontrado una solución. “En vista de su interés”, le escribe Hilbert, “me gustaría presentarle mi teoría con todo detalle el martes. A mi esposa y a mí nos complacería mucho que se quedara en nuestra casa”. ¿”Mi teoría”? Y encima Hilbert añade en posdata: “Hasta donde alcanzo a entender, su solución es completamente distinta de la mía”. Aquello es demasiado. Einstein declina la invitación pretextando cansancio y dolores de estómago y redobla su ritmo de trabajo.
Por fin prueba otra modificación de las ecuaciones que explica bien las irregularidades de Mercurio. La emoción le produce palpitaciones. “Pasé varios días transportado de alegría”, escribirá después en una carta. El 18 de noviembre descubre que el resultado de Hilbert es casi idéntico al suyo. ¡Horror! Tercera conferencia en la Academia Prusiana. Einstein escribe a su rival: “Su sistema coincide exactamente con lo que he descubierto estas semanas y presentado ante la academia. Hoy presentaré un trabajo en el que obtengo cuantitativamente, por medio de la relatividad general, el movimiento del perihelio de Mercurio. Ninguna teoría de la gravitación lo había permitido hasta hoy.” Hilbert contesta amablemente: “Felicidades por conquistar el movimiento del perihelio” y lo felicita también por ser tan veloz para calcular, pero al día siguiente envía a una revista un trabajo con su versión de las ecuaciones.
Einstein culmina sus cuatro conferencias el 25 de noviembre con “Las ecuaciones de campo de la gravitación”, forma final y satisfactoria de la teoría. Con la seguridad de haber ganado la carrera de la prioridad, Einstein puede volver a ser magnánimo: “Ha habido entre nosotros cierta animadversión, cuyas causas no quiero analizar”, le escribe a Hilbert al cabo de unas semanas. “Nuevamente pienso en usted con profunda simpatía y le ruego que haga lo mismo conmigo”. Más tarde, Hilbert se apresurará a señalar: “El trabajo es de Einstein, no de los matemáticos.”p
Examen final
Cien años después del mes más intenso de la vida de Einstein, la teoría general de la relatividad ha superado muchas pruebas. La desviación de la luz se demostró en 1919 y la dilatación del tiempo en un campo gravitacional en 1959. Los satélites del sistema GPS toman en cuenta la diferencia en la marcha del tiempo entre la superficie de la Tierra y la altitud a la que se encuentran. Los hoyos negros, que en los años 30 eran sólo una idea descabellada, hoy se aceptan como predicción confirmada (o casi). La equivalencia entre inercia y gravedad, la idea feliz en la que se asienta la teoría, se ha probado con una precisión de una parte en 10 billones (ya hay planes para llevar la precisión aún más lejos) y la relatividad general es el alma de la teoría del Big Bang del origen del Universo.
Pese a todo, la gran señora de las teorías físicas aún tiene obstáculos por superar. Algunos físicos señalan que hasta hoy sólo se ha probado en situaciones en las que no se destaca de sus rivales, pero la cosa está por cambiar. En 2018 los dos equipos que descubrieron el hoyo negro supermasivo del centro de nuestra galaxia observarán atentamente y con telescopios mejorados una de las estrellas que lo orbitan, que en esa fecha pasará escalofriantemente cerca del objeto. En septiembre pasado empezó a operar la versión mejorada del observatorio de ondas gravitacionales LIGO (véase ¿Cómo ves? No. 68 y No. 195). Las ondas gravitacionales son otra de las predicciones pendientes de la teoría más hermosa de Einstein. Es una época muy emocionante. En los próximos años, el paso de la estrella por el campo gravitacional más intenso de la galaxia y el nuevo detector del observatorio LIGO podrían revelar, por fin, la firma inconfundible de la relatividad general.
O no.
Más información
- Clifford M. Will, ¿Tenía razón Einstein?: la espectacular confirmación científica de la teoría de la relatividad, Gedisa, Barcelona, 1989.
- Michio Kaku, El Universo de Einstein: cómo la visión de Albert Einstein transformó nuestra comprensión del espacio y el tiempo, Antonio Bosch, 2005.
- Shahen Hacyan, Los hoyos negros y la curvatura del espacio-tiempo, FCE, México, 1997.
Sergio de Régules es coordinador científico de ¿Cómo ves? Su libro más reciente es El universo en un calcetín (Ediciones B México, 2015).














