El mundo no es como lo pintan: mentiras y verdades de un mapa*
Sergio de Régules
¿Cómo ves?
El abuso de un mapa originalmente concebido para hacerles la vida fácil a los navegantes nos ha dado una imagen distorsionada de la geografía de la Tierra.
El pesado Galeón conocido como la Nao de China se apresta a zarpar del puerto novohispano de Acapulco con destino a Manila, en las islas Filipinas. El capitán se acaricia las barbas. Es su primer viaje a Oriente.
—Hum... —dice. Y no es para menos: está a punto de emprender una travesía larga y peligrosa. El océano equivocadamente llamado Pacífico es traicionero y allá, en altamar, aguardan los piratas.
—Hum, hum... —dice el capitán. Más que las marejadas y los filibusteros le preocupa un problema práctico que se enuncia en cuatro palabras:
¿Hacia dónde está Manila?
 Planisferio según la proyección de Mercator, 1780.
Planisferio según la proyección de Mercator, 1780.
El imperio de la brújula
Por suerte el capitán, aunque novato, cuenta con todo el arsenal del marino moderno (del siglo XVII). En una cubierta inferior de la Nao, junto al timón, se encuentra la bitácora, armario en el que se guarda la brújula. Al lado de la bitácora hay otro armario atestado de mapas. La brújula y los mapas son el tesoro más preciado del marino.
El capitán saca un rollo y lo extiende sobre una mesa, sujeta las esquinas del plano con lo primero que encuentra y dice:
—Hum, hum, hum... Ante sus ojos se encuentra la máxima maravilla de la cartografía: el mapa que el cartógrafo flamenco Gerard Mercator publicó en 1569. Es un mapa hecho especialmente para la navegación, pilar de la economía del mundo de la época. La imagen de los accidentes geográficos que pinta el mapa atiende únicamente a los intereses y preocupaciones de los navegantes. Éstos sólo quieren saber qué rumbo tomar para ir del puerto A al puerto B. No les interesa si África es más extensa que Rusia, ni cómo se compara en área Europa con el Reino del Perú. Los tamaños relativos de países y continentes son cosa de estudiosos, no de marinos.
Tampoco les interesa saber cuál es el camino más corto entre A y B, sino cuál es el más fácil, dados los instrumentos de navegación con los que cuentan en esa época. Uno de los más importantes es, desde luego, la brújula. La forma más fácil de navegar de un puerto a otro en el siglo XVII es seguir una misma dirección de la brújula, sin desviaciones; es decir, navegar por una trayectoria de rumbo fijo.
Pero, ¿qué rumbo fijo seguir para llegar de Acapulco a Manila? El mapa de Mercator, esa joya cartográfica, proporciona la información deseada. El capitán toma un trozo de carbón y una regla, la tiende sobre el mapa entre los dos puertos y traza una recta. La orientación de esa recta da el rumbo fijo que hay que seguir.
Con esta información, bien lo sabe el capitán, se orienta la nave en la dirección indicada, se mantiene el rumbo fijo según la brújula, se espera el tiempo suficiente y se acaba por llegar, si no lo impiden las tormentas ni los piratas.
 Versión moderna del mapa del mundo de Gerard Mercator, un mapa hecho para facilitarles la vida a los navegantes que usaban brújula.
Versión moderna del mapa del mundo de Gerard Mercator, un mapa hecho para facilitarles la vida a los navegantes que usaban brújula.
Geometría esférica
La operación de trazar la recta que une origen y destino para saber hacia dónde dirigirse quizá te parezca sencilla y hasta evidente. Después de todo, en un plano la distancia más corta entre dos puntos es el segmento de recta que los une, y para ir del uno al otro basta seguir esa recta sin desviarse. ¿Por qué habrían de ser distintas las cosas en un mapa?
Porque un mapa es un plano, en efecto, pero un plano que representa la superficie esférica de la Tierra. En las esferas, las líneas y figuras de la geometría plana tradicional que nos enseñan en la escuela se comportan de maneras extrañas. Por ejemplo, en el plano la suma de los ángulos internos de cualquier triángulo siempre es igual a 180°. En la esfera, en cambio, la suma de los ángulos internos de un triángulo siempre es mayor que 180°.
Las rectas también se toman ciertas libertades al pasar del plano a la esfera, de modo que lo que es recta en el mapa será otra cosa en la esfera de la Tierra. ¿Qué otra cosa? Eso depende de la proyección que se haya empleado para trazar el mapa. La proyección es la manera particular en que se llevan los puntos de la esfera al plano, y las hay de muchos tipos. El cartógrafo usa la proyección que más conviene al propósito de su mapa. La proyección de Gerard Mercator tiene la gracia de transformar en rectas las trayectorias de rumbo fijo, pero en la superficie terrestre éstas no son rectas. ¿Qué son entonces?
 Triángulo esférico formado por dos segmentos de meridiano y un segmento del ecuador. Como cada meridiano forma un ángulo de 90˚ con el ecuador, la suma de los ángulos internos de este triángulo es mayor que 180˚. Lo mismo se puede decir de todos los triángulos esféricos.
Triángulo esférico formado por dos segmentos de meridiano y un segmento del ecuador. Como cada meridiano forma un ángulo de 90˚ con el ecuador, la suma de los ángulos internos de este triángulo es mayor que 180˚. Lo mismo se puede decir de todos los triángulos esféricos.
 Trayectoria de rumbo fijo en la proyección de Mercator: una línea recta.
Trayectoria de rumbo fijo en la proyección de Mercator: una línea recta.
Trayectorias de rumbo fijo
Los matemáticos saben qué forma tienen las trayectorias de rumbo fijo en la esfera por lo menos desde 1550, pero yo lo descubrí por accidente y de la manera más insólita hace apenas unos años. Les contaré.
Soy fanático del simulador de vuelo de cierta compañía de software archiconocida, lo confieso sin vergüenza. Un día, adquiridas ya las habilidades de control y navegación del avión virtual —y con muchas horas de ocio por delante—, se me ocurrió hacer el vuelo México-París en tiempo real. El programa no contempla esta clase de locuras (me imagino que no debe ser normal estar dispuesto a pasarse quién sabe cuántas horas delante de la computadora esencialmente sin hacer nada). No hay en su mundo virtual radiofaros suficientes para un vuelo tan largo (un radiofaro emite una señal de radio que permite a los pilotos orientarse). Tampoco hay nada que indique el rumbo a seguir. Pero pulsando un botón sale en la pantalla de la computadora un mapa con la siguiente propiedad: el avión siempre aparece al centro, orientado hacia arriba; el resto del mundo se distribuye a su alrededor en un disco. Cuando el avión da vuelta, es el mundo el que gira. (No me di cuenta en ese momento de que lo que tenía ante los ojos era un mapa en una proyección interesantísima, de la cual les hablaré más adelante).
De modo que viré hacia la derecha y esperé a que París se pusiera justo enfrente de mi avión, lo cual ocurrió cuando la nave alcanzó el rumbo del Noreste, rumbo que abreviaremos así: E 45° N, y que forma un ángulo de 45° con la dirección Norte. Hecho esto, programé el piloto automático para que conservara ese rumbo y fui a hacerme un café.
Bebido el café, consulto el mapa y observo con asombro que el avión ya no se dirige a París. Qué raro. Corrijo el curso con el mismo método: virando hacia la derecha y esperando a que París se me ponga enfrente. Reprogramo el piloto automático para seguir el nuevo rumbo y me pongo a leer.
Al rato, lo mismo: el avión va fuera de curso. ¿Qué pasa? ¿No sirve el piloto automático? Entonces se me conecta el cerebro: el piloto automático sí sirve y está haciendo su trabajo a las mil maravillas, ¡pero la Tierra es redonda! (No me digan que ya lo sabían…).
Cuando un avión vuela con rumbo fijo su trayectoria forma el mismo ángulo con todos los meridianos que cruza, sin importar la latitud. Se encuentre donde se encuentre —en el ecuador o en las regiones polares—, mi avión debe cortar los meridianos a 45° para dirigirse siempre al Noreste. En el mapa de Mercator los meridianos son rectas paralelas, de modo que la trayectoria de rumbo constante E 45° N es una recta inclinada a 45°.
Pero en la superficie esférica de la Tierra los meridianos convergen en un punto en los polos. Para cortar los meridianos con el mismo ángulo en todas partes, la trayectoria del avión tiene que torcerse continuamente hacia el polo conforme aumenta la latitud.
Para entonces he perdido interés en ir a París (por lo menos virtualmente) y me dispongo a comprobar si sucede lo que creo que sucede si dejo volar mi avión en piloto automático hasta las regiones polares. Al cabo de muchas horas, cuando la crucecita que indica la posición del avión en el mapa está muy cerca del Polo Norte, el disco mundial empieza a girar más y más rápido: el avión se aproxima al polo en círculos cada vez más apretados. ¡He descubierto que en la esfera las trayectorias de rumbo fijo son espirales que se enroscan alrededor de los polos sin jamás tocarlos! (¿Quién dijo que los videojuegos eran una pérdida de tiempo?)
Desde luego, en la práctica, uno nunca sigue una trayectoria de rumbo fijo en toda su extensión (que, por cierto, es infinita porque la curva nunca llega al polo), sino sólo un segmento.
 Trayectoria de rumbo fijo en la superficie terrestre: una espiral que se enrosca alrededor de los polos.
Trayectoria de rumbo fijo en la superficie terrestre: una espiral que se enrosca alrededor de los polos.
 Dos rutas de México, D.F. a Madrid. La recta es la trayectoria de rumbo fijo (loxodromia), la curva es el segmento de círculo máximo (geodésica). Aunque en el mapa de Mercator la geodésica se ve más larga, es más corta en la superficie terrestre (loxodromia = 9 411 kilómetros, geodésica = 9 068 kilómetros).
Dos rutas de México, D.F. a Madrid. La recta es la trayectoria de rumbo fijo (loxodromia), la curva es el segmento de círculo máximo (geodésica). Aunque en el mapa de Mercator la geodésica se ve más larga, es más corta en la superficie terrestre (loxodromia = 9 411 kilómetros, geodésica = 9 068 kilómetros).
Las curvas menos curvas
Las trayectorias de rumbo fijo también se llaman loxodromias (de loxós, oblicuo, y dromos, carrera). Las estudió el matemático y cartógrafo portugués Pedro Nunes en 1550. Nunes pensaba que la distancia más corta entre dos puntos de la superficie terrestre era el segmento de loxodromia que los une, lo cual parece muy razonable —sobre todo sabiendo que los rumbos fijos se transforman en rectas en el mapa de Mercator—, pero es falso. Las loxodromias te llevarán de A a B por el camino más fácil, pero no el más corto.
El camino más corto entre dos puntos de la esfera es un segmento de la curva menos curva que se puede trazar en una superficie esférica: el círculo máximo. En una pelota puedes dibujar círculos de muchos tamaños, pero los más grandes posibles —los círculos máximos— son los que tienen el mismo diámetro que la pelota.
Los meridianos y el ecuador son círculos máximos de la superficie terrestre, pero hay una infinidad de círculos máximos posibles, orientados no sólo de Norte a Sur y de Este a Oeste, sino en todas direcciones. Es más, dados dos puntos cualesquiera de la superficie terrestre, siempre se puede encontrar un círculo máximo que pasa por ambos. El segmento de círculo máximo que los une es el camino más corto entre esos puntos.
Fíjate cómo se parece este resultado al teorema de geometría plana que dice que entre dos puntos del plano siempre se puede trazar una recta y que la distancia más corta entre dos puntos es el segmento de recta que los une. En la esfera o en el plano (o, en general, en cualquier espacio, pero eso es harina de otro costal) las curvas que dan la distancia mínima entre dos puntos se llaman geodésicas. Las rectas son las geodésicas del plano, los círculos máximos son las geodésicas de la esfera. Como sería de esperarse, en el mapa de Mercator los círculos máximos no están representados como rectas (con excepción de los meridianos y el ecuador).
 Los caminos más cortos de México, D.F. a todas partes. Las líneas que salen de la ciudad son círculos máximos, es decir, trayectorias de distancia mínima. Las otras curvas representan puntos que están a una misma distancia de la Ciudad de México. Los círculos máximos se juntan de nuevo en las antípodas, el lugar al que llegarías si cavaras un hoyo que atravesara la Tierra por el centro (por cierto, ¡no es China!). Detalle curiosísimo: los segmentos que van de la ciudad a sus antípodas son todos de la misma longitud en la esfera, lo cual no es nada evidente en la proyección de Mercator.
Los caminos más cortos de México, D.F. a todas partes. Las líneas que salen de la ciudad son círculos máximos, es decir, trayectorias de distancia mínima. Las otras curvas representan puntos que están a una misma distancia de la Ciudad de México. Los círculos máximos se juntan de nuevo en las antípodas, el lugar al que llegarías si cavaras un hoyo que atravesara la Tierra por el centro (por cierto, ¡no es China!). Detalle curiosísimo: los segmentos que van de la ciudad a sus antípodas son todos de la misma longitud en la esfera, lo cual no es nada evidente en la proyección de Mercator.
 ¿Qué ciudad está más lejos? En la proyección de Mercator San Petersburgo se ve más lejos de la Ciudad de México que Roma, pero a lo largo de círculos máximos San Petersburgo está a 10 093 kilómetros y Roma a 10 250 kilómetros. El mapa de Mercator distorsiona las distancias, sobre todo en latitudes elevadas.
¿Qué ciudad está más lejos? En la proyección de Mercator San Petersburgo se ve más lejos de la Ciudad de México que Roma, pero a lo largo de círculos máximos San Petersburgo está a 10 093 kilómetros y Roma a 10 250 kilómetros. El mapa de Mercator distorsiona las distancias, sobre todo en latitudes elevadas.
La joya de la cartografía
Que la distancia mínima entre dos puntos de la Tierra es un segmento de círculo máximo ya lo sabían los matemáticos de antes de la época de Cristóbal Colón (aunque, al parecer, Pedro Nunes lo ignoraba en 1550), pero fue hasta el siglo XVIII cuando la técnica permitió calcular los rumbos perpetuamente cambiantes de una ruta geodésica. Hasta entonces los marinos se conformaron con emplear rutas de rumbo fijo.
Para enderezar los rumbos fijos Mercator enderezó primero los meridianos convirtiéndolos en rectas verticales paralelas que se extendían hasta el infinito. Con esta operación introdujo una distorsión de las distancias en la dirección Este-Oeste que aumentaba de nula en el ecuador (donde no había sido necesario hacerles nada a los meridianos) a infinita en los polos. Al separar los meridianos en forma creciente con la latitud, Mercator deformó los continentes en el sentido horizontal como si fueran figuras pintadas en una membrana de hule que se estira hacia los lados. Para corregir la deformación se vio obligado a estirar cada grado de latitud en la misma proporción en que había estirado los de longitud para enderezar los meridianos. Como resultado de estas manipulaciones las loxodromias se convertían en rectas, pero las distancias (y por lo tanto los tamaños de los continentes) se inflaban desmesuradamente en las latitudes superiores. Ni modo. Si quería mostrar los rumbos fijos como rectas, tenía que sacrificar la veracidad de las distancias.
Eso quiere decir que los tamaños de los continentes en el mapa de Mercator son puras mentiras. Alaska no es más extensa que México ni Europa más que Sudamérica, como puedes comprobar consultando un globo terráqueo. Pero a Mercator y sus clientes, los marinos, no les interesaban los tamaños relativos de las tierras, sino las direcciones relativas, y ésas sí se conservan en el mapa de Mercator. Los cartógrafos no mienten por maldad, sino por necesidad. Es matemáticamente imposible hacer un mapa plano sin introducir deformaciones. El cartógrafo escoge cómo va a mentir según el propósito de su mapa. Mercator quería conservar las direcciones y para eso tuvo que sacrificar las distancias.
 Mapamundi de Battista Agnese, 1540.
Mapamundi de Battista Agnese, 1540.
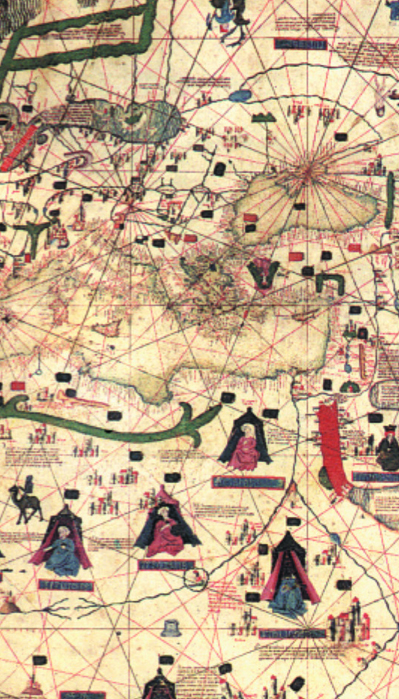
 Planisferio de Cantino, 1502.
Planisferio de Cantino, 1502.
La metáfora extendida
El mapa de Mercator adquirió mucha popularidad y prestigio en los siglos XVII y XVIII. Era el mapa de los navegantes y éstos gozaban de mucha estimación en una época en que el barco era el medio de transporte más socorrido, tanto para mercancías valiosas como para ejércitos conquistadores.
Junto con su religión y cultura (y codicia y violencia, hay que decirlo), las naciones europeas de la época colonial llevaron a las tierras conquistadas su mapa preferido. Con el tiempo, el mapa que Gerard Mercator ideó inocentemente en el siglo XVI para ayudar a los navegantes, y que era uno de tantos mapas del mundo, se impuso —con sus verdades y mentiras— como la descripción por antonomasia de todas las tierras del orbe.
Un mapa es una metáfora. No es el mundo, sólo una representación del mundo, e inevitablemente muestra sólo uno de los muchos aspectos de lo representado. Si lo quieres ver desde otra perspectiva necesitas otro mapa. Un mapa, como una metáfora, dice verdades en cierto contexto y mentiras fuera de él.
La proyección de Mercator trascendió el mundillo de marinos y navegantes y se empleó para todo. Extraída del contexto en el que surgió, produjo equívocos que persisten hasta hoy. En mi escuela había mapas colgados en las paredes. Todos eran proyecciones de Mercator, por lo tanto durante mucho tiempo viví convencido de que Groenlandia era la isla más grande del mundo y de que la Antártida superaba en área a los demás continentes juntos. ¿Te pasó a ti también?
Por supuesto, Mercator no tiene la culpa de nuestras falsas impresiones geográficas. La culpa es de las vicisitudes de la historia, que elevaron su mapa a una posición que ni buscaba ni se merecía, y que hicieron olvidar a muchas personas que, como dice Lloyd A. Brown, autor de un libro de historia de la cartografía, "no existe el mapa ideal, bueno para cualquier propósito; toda proyección tiene que sacrificar la exactitud y tolerar distorsiones de uno u otro tipo".
Si tú también has caído en la trampa involuntaria de Mercator, te invito a consultar un globo terráqueo y hacer comparaciones. Te vas a llevar varias sorpresas.
Sorpresas geográficas
Hechos asombrosos que sólo nos parecen asombrosos por estar acostumbrados a la proyección de Mercator. Compruébalos usando el mapa acimutal equidistante.
- Roma está más lejos de México que San Petersburgo.
- Cualquier punto del sur de Italia está más lejos de nosotros que cualquier punto de Finlandia.
- Córcega y Cerdeña, en el mar Mediterráneo, están a la misma distancia que la Península Antártica y la isla Sajalin.
- El camino más corto de la Ciudad de México a la India y Sri Lanka es hacia el norte, pasando por el polo.
- El camino más corto a Japón pasa por el norte de California y las islas Aleutianas.
- Europa está más lejos que el Polo Norte.
- El punto más alejado de la Ciudad de México (sus antípodas) se encuentra en medio del océano Índico.
- Para viajar a las antípodas por el camino más corto no importa en qué dirección partamos.
- La distancia de cualquier punto a sus antípodas sobre la superficie de la Tierra es de unos 20 000 kilómetros. Si pudiéramos ir allí atravesando el centro del planeta tendríamos que recorrer sólo 12 800 kilómetros (el diámetro del planeta).
 Mapa acimutal equidistante centrado en la Ciudad de México. En esta proyección las trayectorias mínimas desde el centro del mapa son rectas. Las regiones que están más lejos de la Ciudad de México están muy aumentadas: Madagascar se ve más grande que Sudamérica. Todos los mapas deforman los continentes de alguna manera.
Mapa acimutal equidistante centrado en la Ciudad de México. En esta proyección las trayectorias mínimas desde el centro del mapa son rectas. Las regiones que están más lejos de la Ciudad de México están muy aumentadas: Madagascar se ve más grande que Sudamérica. Todos los mapas deforman los continentes de alguna manera.
Otro mapa
Y hablando de sorpresas… Hace dos años encontré en Internet el programa Globe (se distribuye gratuitamente en esta dirección: www.beanpaste.com/BSG/globe. htm), que sirve para trazar trayectorias loxodrómicas y geodésicas en la superficie terrestre y que usé como base para hacer los mapas de este artículo. Entre las diversas proyecciones cartográficas que contiene como opciones se encuentra la llamada proyección acimutal equidistante, que resulta ser precisamente la que vi en la pantalla de mi computadora aquel día aciago en que se me ocurrió volar a París.
La proyección acimutal equidistante, que ideó el matemático árabe Al-Biruni hace mil años, se hace escogiendo un centro y proyectando el resto del mundo a su alrededor de tal manera que toda recta trazada desde el centro sea un círculo máximo y que las distancias desde el centro estén correctamente representadas. Cuando orienté mi avión hacia París en el simulador de vuelo estaba enfilando la trayectoria de distancia mínima a París, no la de rumbo fijo. Por lo general, para seguir una trayectoria de distancia mínima hay que cambiar de rumbo constantemente. ¡Por eso el avión se desviaba de la ruta indicada cuando volaba en piloto automático!
Sergio de Régules siguió una trayectoria geodésica de la física a la divulgación de la ciencia. Es autor de los libros El Sol muerto de ris, El renovador involuntario, Cuentos cuánticos y El piropo matemático. Trabaja en el Museo Universum.














