Retos 316
Aquí tod@s estamos loc@s
Claudia Hernández García

Ilustración: Santiago Solís Montes de Oca
Estoy casi segura de que la mayoría de ustedes sabe que el libro Alicia en el país de las maravillas fue escrito por Lewis Carroll. Lo que probablemente no sepan es que su nombre real era Charles Lutwidge Dodgson y que fue clérigo, fotógrafo y matemático, profesor de la Universidad de Oxford. El pseudónimo está compuesto de la siguiente manera: Lewis viene de Lutwidge y Carroll de Charles, aunque también se inventó un par de nombres más elaborados, ambos anagramas de Charles Lutwidge: Edgar Cuthwellis y Edgar U. C. Westhill. Lo de los anagramas no es un hecho aislado: a Carroll le encantaba inventar acertijos. En el capítulo vii, el Sombrerero Loco enuncia uno muy famoso: ¿en qué se parecen un cuervo y un escritorio? A ver, ¿en qué creen que se parezcan?
Escalera de palabras
Otro de sus famosos retos consiste en transformar una palabra en otra cambiando una letra a la vez, cuidando que todas las nuevas combinaciones tengan significado y sin agregar ni quitar letras en ningún paso. Por ejemplo, la palabra sol se puede transformar en mar con estos pasos: sol-sal-mal-mar. El primer reto será uno doble y consiste en ir de roca a niño y de brasa a fruta siguiendo esas reglas.
Carroll los llamaba escaleras de palabras (word ladders) porque iba acomodando las palabras de arriba hacia abajo y consideraba que era preferible una solución con menos escalones. Si te animas a resolver la escalera original que publicó en Vanity Fair en 1867 hay que ir de head a tail.
Pasteles en fila
Muchos de los acertijos que inventaba Carroll venían acompañados de una historia que les daba contexto. Para el siguiente reto (originalmente titulado Cakes in a row) no rescataré la historia previa sobre unas piedras que Alicia veía convertirse en pasteles, pero sí las indicaciones.
Aquí hay dos filas con cinco pasteles (o piedras) que conservan la misma distancia entre sí. Reacomoda los pasteles para hacer cinco filas que contengan cuatro pasteles cada una. Sólo puedes cambiar cuatro pasteles de posición.

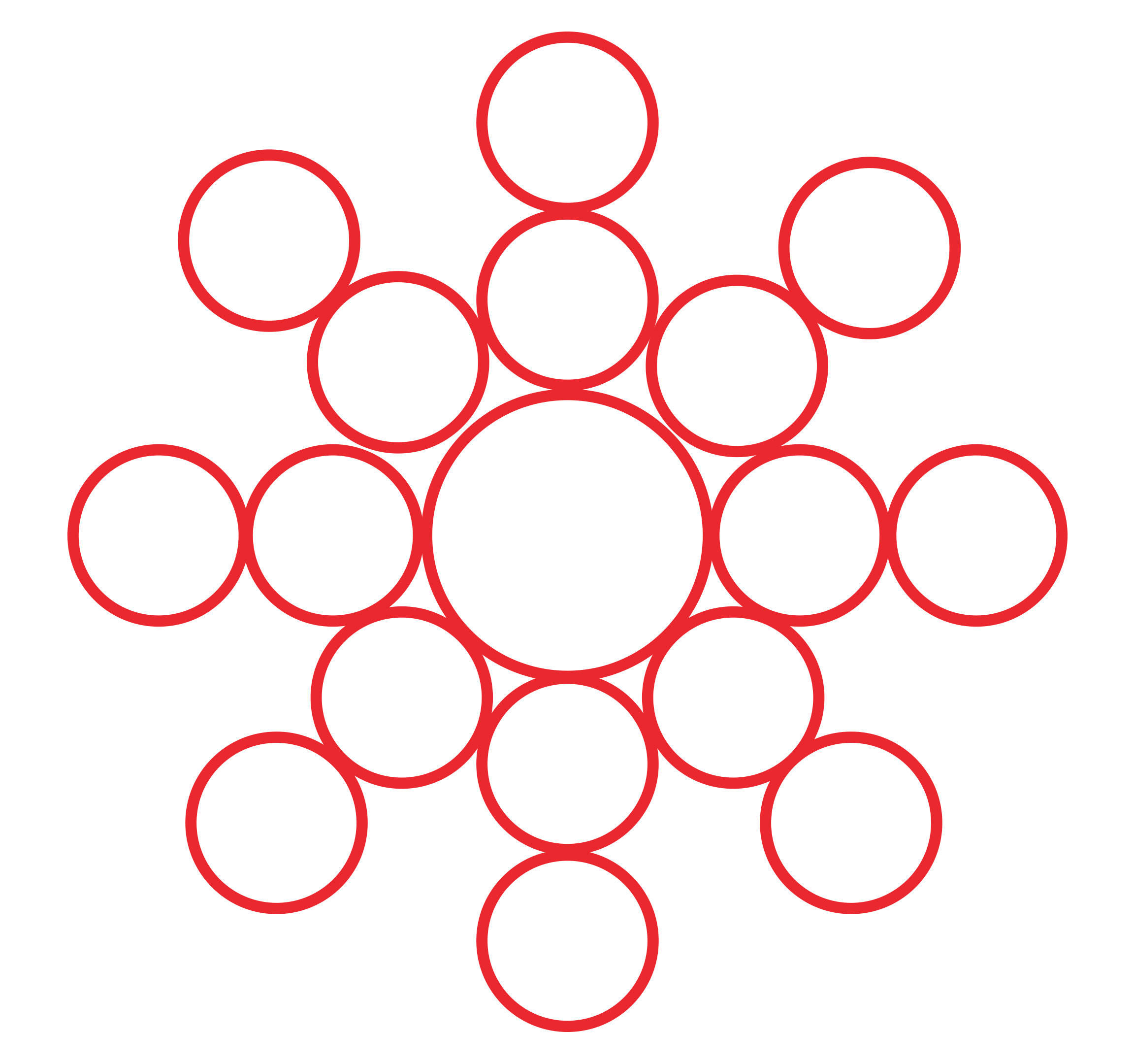
Avanzando en círculos
El último reto es uno que Carroll escribió en una hoja de papel con fecha del 9 de abril de 1889. Consiste en redibujar esta composición de circunferencias con un solo trazo, con la regla de que cada vez que lleguen a un punto de contacto cambien de circunferencia y nunca retrocedan en su recorrido.
Que Carroll no haya aclarado en el libro en qué se parecen un cuervo y un escritorio causó revuelo en la época, y por ello se vio obligado a proporcionar la siguiente respuesta en el prefacio de una edición posterior: “en que ambos pueden producir algunas notas, aunque muy planas”. Tampoco reconoció que tuvo que inventarlo después, porque originalmente no había concebido una solución para el acertijo. Si les interesa conocer un poco más sobre Lewis Carroll o la ciencia a la que hacía referencia les sugiero el artículo “Alicia y el país de las maravillas científicas”, de Luis Javier Plata Rosas, en ¿Cómo ves?, núm. 137.
Soluciones núm. 315
En orden y sin repetir. Una forma de llevar un orden al contar es a partir del tamaño de los cuadrados. Yo imagino que los acomodo primero horizontalmente y luego verticalmente, moviéndolos un cuadro a la vez. Con esta técnica conté 30 cuadrados en total: 16 de 1 × 1 como el naranja, nueve de 2 × 2 como el amarillo, cuatro de 3 × 3 como el verde y uno de 4 × 4 que los contiene a todos.

Otros poquitos. En la imagen hay 40 cuadrados, los mismos del reto anterior y estos diez adicionales:

Más allá de los cuadrados. Esta solución puede generar confusión porque luego se nos olvida que los cuadrados también son rectángulos. Entonces, yo digo que esta imagen contiene 100 rectángulos, los 30 cuadrados de todos los tamaños y estos otros 70: 24 como el rojo de 1 × 2 (vertical) o 2 × 1 (horizontal), 16 como el rosa de 1 x 3 o 3 × 1, 8 como el café de 1 × 4 o 4 × 1, 12 como el azul de 2 × 3 o 3 × 2, 6 como el beige de 2 × 4 o 4 × 2 y 4 como el gris de 3 × 4 o 4 × 3.

El pilón. Yo encontré 36 heptágonos, 9 de cada uno de los señalados a continuación. Si ustedes encontraron otros, entonces mi estrategia de conteo no fue tan buena. Compártanme en redes los otros heptágonos que hayan detectado.
















