El sueño de la computación cuántica
Daniel Martín Reina

Jon Simon/Feature Photo Service - IBM
Las computadoras cuánticas prometen revolucionar la ciencia y la tecnología. En la última década, este campo ha recibido un importante impulso por parte de grupos de investigación y empresas emergentes de todo el mundo.
En 1981 se celebró en el Instituto Tecnológico de Massachusetts la Primera Conferencia sobre Física Computacional. El físico estadounidense Richard Feynman abrió el congreso hablando de un campo de investigación en pleno auge: la simulación de sistemas físicos mediante computadora. Los fenómenos naturales en la escala más pequeña, razonó Feynman, siguen las reglas de la física cuántica, que es muy diferente de la física a la que estamos acostumbrados, conocida como clásica. Tan diferentes son, que nunca podremos simular fenómenos cuánticos con computadoras clásicas. Feynman terminó su charla desafiando a los allí presentes a desarrollar una nueva clase de computadoras basadas en la física de lo muy pequeño. Así surgió el sueño de la computación cuántica.
Hoy, 38 años después de aquella histórica charla, la participación de gigantes tecnológicos como Google, IBM y Microsoft nos ha acercado más que nunca a superar el desafío de Feynman.
Limitaciones actuales
Todas las computadoras actuales operan de acuerdo con las leyes de la física clásica. Y según estas, el elemento de memoria fundamental de una computadora, el bit, sólo puede tener valores bien definidos, 0 o 1, sin ambigüedades. En la práctica, los bits están encarnados en dispositivos electrónicos llamados transistores. Los estados 0 y 1 se representan como un interruptor que corta o deja pasar la corriente eléctrica. Juntando varios bits podemos representar números y hacer operaciones con ellos. Eso sí, con algunas limitaciones: si tenemos n bits, podemos representar hasta 2n estados distintos (con 10 bits, 1 024 estados; con 20 bits, 1 048 576; con 30, 1 073 741 824), pero solo los podemos manipular uno a la vez. Es decir, por muy rápida que sea una computadora, únicamente puede tratar una cuestión al mismo tiempo. Si el problema requiere tratar muchas (casi todos los problemas conllevan muchos pasos), estas se consideran de una en una, en secuencia.
Según la llamada ley de Moore, propuesta en 1965 por el fundador de Intel, Gordon Moore, cada dos años se reduce a la mitad el tamaño de los transistores. Esto significa que cada dos años se puede duplicar el número de transistores que componen una computadora, lo que hace aumentar su potencia y eficiencia. Las computadoras de hoy tienen cientos de millones de transistores de un tamaño del orden del nanómetro (la milmillonésima parte de un metro), miles de veces más diminutos que el grosor de un cabello humano. Pero no podemos hacer los transistores infinitamente pequeños. Hay un límite a partir del cual dejan de funcionar correctamente, víctimas de efectos cuánticos, y ya estamos muy cerca de alcanzar ese límite. Además, mientras más transistores tiene la computadora, más difícil es disipar el calor que generan. Buena parte de la energía consumida por las computadoras está dedicada a enfriarlas, pues de lo contrario se calentarían en exceso y se dañarían.
Aunque la computación clásica está a punto de tocar techo, todavía hay problemas computacionales que por su complejidad quedan fuera de su alcance. Por ejemplo, es imposible modelar el comportamiento de moléculas relativamente sencillas como la cafeína (cuya fórmula es C8H10N4O2) porque estas tienen tantos posibles estados cuánticos, que ni la computadora más potente de la actualidad puede considerarlos todos en un tiempo razonable.
Una nueva computación
Aquí es donde entra en juego la computación cuántica, que podría aprovechar algunas de las extrañas propiedades de la física cuántica, la teoría que gobierna el mundo del átomo y su interior. Un bit cuántico, o cúbit, tiene más posibilidades de almacenar información que uno clásico porque, además de los dos estados clásicos 0 y 1, puede encontrarse en combinaciones de ambos. Dicho de otra manera, puede estar parcialmente en uno y otro al mismo tiempo. Esto implica que, a diferencia de la computadora clásica, la computadora cuántica sí puede ejecutar varios pasos a la vez.
El verdadero potencial de una computadora cuántica surge cuando dispone de más de un cúbit. En una computadora clásica, los bits funcionan de manera independiente. Si disponemos de dos transistores, cada uno puede estar “abierto” o “cerrado”, y el estado de uno no depende del estado del otro. En una computadora cuántica, en cambio, diferentes cúbits pueden estar entrelazados.
El entrelazamiento cuántico es uno de los fenómenos físicos más sorprendentes que se conocen (véase ¿Cómo ves?, Núms. 67 y 205). Cuando dos partículas están entrelazadas, las propiedades de una afectan instantáneamente a las de la otra, por muy separadas que se encuentren. Imaginemos que tenemos dos monedas cuánticas entrelazadas. Si lanzamos ambas y observamos que una cae en “águila”, podemos estar seguros de que la otra adquiere el opuesto y cae en “sol”, aunque esa moneda se encuentre muy lejos. El entrelazamiento es lo que hace posible que las computadoras cuánticas sean tan potentes. En una computadora clásica, es necesario realizar una operación básica por cada bit que queramos cambiar, pues estos son independientes. En el caso de una computadora con cúbits entrelazados existen operaciones básicas que modifican el estado de varios cúbits a la vez. Esto permite ejecutar programas con más eficiencia, básicamente porque la computadora cuántica tiene que hacer menos operaciones que una clásica. Eso sí: los programas tienen que escribirse de forma especial, como algoritmos cuánticos.
Bit
Las computadoras actuales operan de acuerdo con las leyes de la física clásica. Por consiguiente, el elemento de memoria fundamental de una computadora, el bit, sólo puede tener valores bien definidos: 0 o 1.
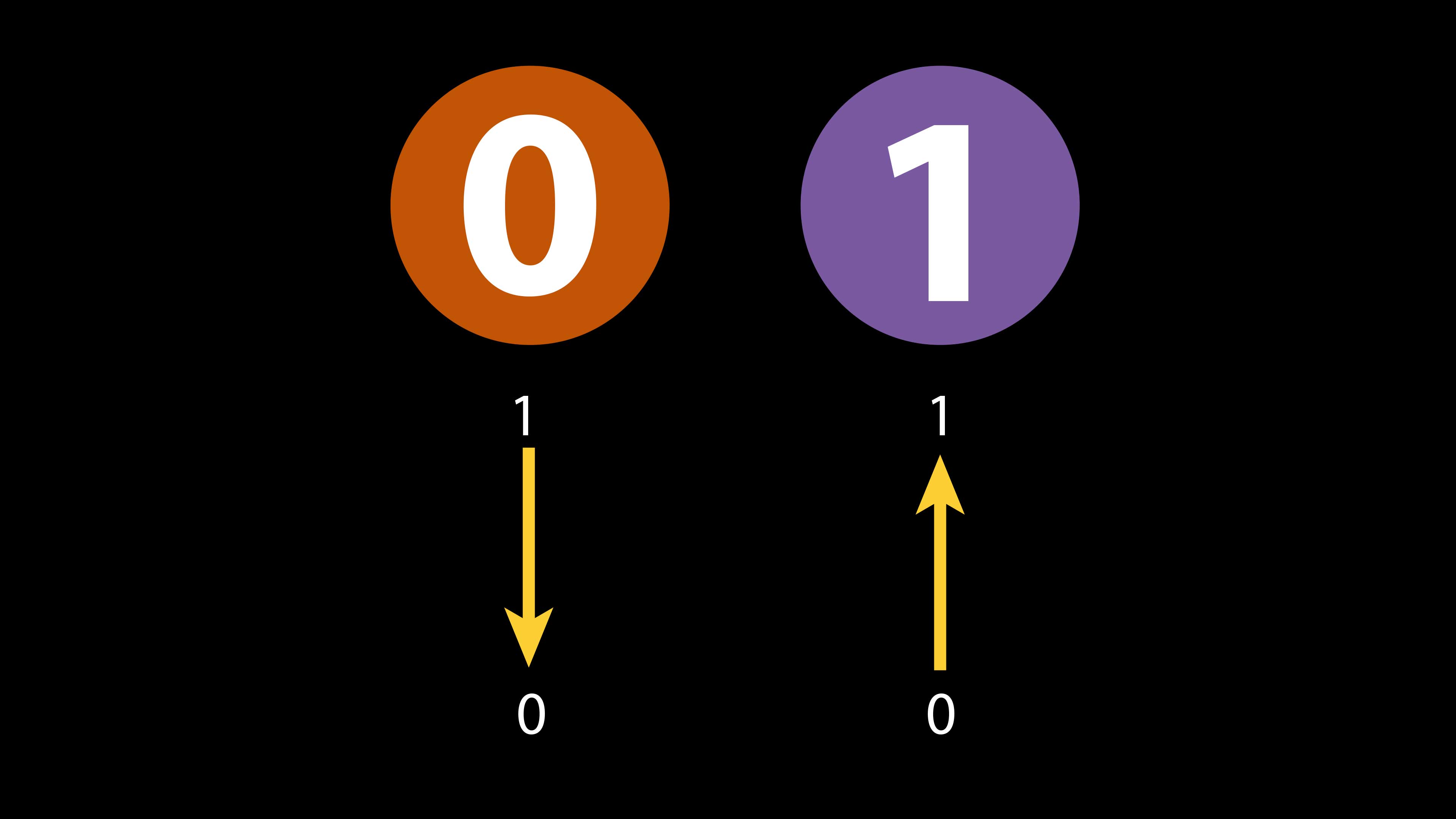
Un bit clásico puede ser 0 o 1. 0 = falso/apagado 1 = cierto/encendido
Bit cuántico (cúbit)
La computación cuántica aprovecha algunas de las extrañas propiedades de la física cuántica, la teoría que gobierna el mundo del átomo y su interior. Así, un cúbit tiene más posibilidades de almacenar información que uno clásico porque, además de los dos estados clásicos 0 y 1, puede encontrarse en combinaciones de ambos.
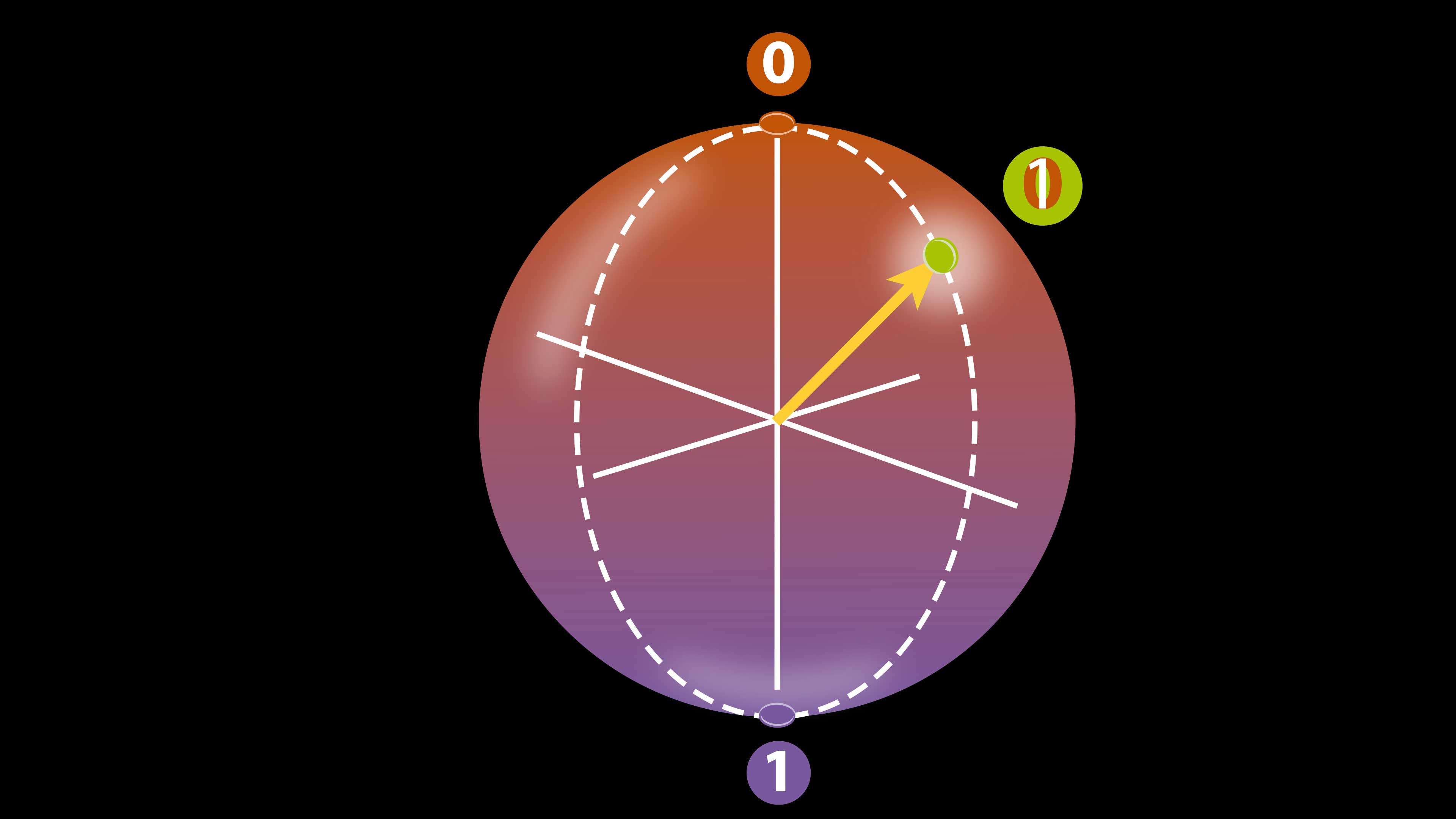
Un cúbit puede estar en un estado de 0 o 1 pero también en una superposición de estados.
Una Experiencia Cuántica
En mayo de 2016 IBM puso en marcha una iniciativa para acercar la computación cuántica a todo aquel que estuviera interesado en ella. La llamada IBM Q Experience ofrecía acceso gratuito a una plataforma de computación cuántica mediante un servicio en la nube en el que se podían ejecutar algoritmos en una computadora cuántica de cinco cúbits. El gigante azul ponía a disposición de los usuarios una interfaz gráfica para programar la computadora cuántica, así como tutoriales y ejemplos para familiarizarse con el entorno de desarrollo.
La iniciativa fue un éxito. En apenas un año, se calcula que unos 40 000 usuarios de más de 100 países desarrollaron cerca de 300 000 algoritmos cuánticos para dicha computadora. Los algoritmos se verificaban primero en un simulador, para luego ejecutarse directamente en la computadora. Gracias a esta enorme cantidad de experimentos se puede validar que la IBM Q de cinco cúbits se comporta como debe y es capaz de realizar múltiples tareas. Todos salen ganando: los usuarios pueden utilizar una computadora que hasta entonces solo estaba al alcance de unos pocos laboratorios en el mundo, e IBM se beneficia del talento de miles de usuarios que diseñan algoritmos e impulsan de esta manera la computación cuántica.
Actualmente hay tres computadoras a disposición de los usuarios: otra igual de cinco cúbits y una tercera de 16. Al mismo tiempo, la comunidad no ha dejado de aumentar: el número de usuarios ha superado los 80 000, y se han ejecutado más de 14 millones de experimentos. Muchos de estos usuarios son investigadores que han compartido en artículos académicos su experiencia con esta herramienta. Profesores de universidad también están incluyendo ejemplos en sus temarios, una buena forma de introducir a los alumnos en este novedoso mundo. Todo ello está logrando que el campo crezca de forma espectacular y empiece a interesar a los más jóvenes. En sus manos está el futuro de la computación cuántica.
 Investigadoras de IBM examinan los sistemas de enfriamiento de la computadora cuántica.
Investigadoras de IBM examinan los sistemas de enfriamiento de la computadora cuántica.
Algoritmos cuánticos
El tiempo que tarda una computadora clásica en factorizar un número de n cifras —es decir, descomponerlo en un producto de números primos— crece exponencialmente con el número de cifras. Así, factorizar un número de 500 cifras requiere 100 millones más de operaciones que factorizar un número de 250 cifras. En 1994 el matemático estadounidense Peter Shor desarrolló un algoritmo cuántico que reducía notablemente el número de pasos a realizar. Gracias al algoritmo de Shor, un número de 500 cifras sólo necesita ocho veces más operaciones que un número de 250 cifras. El potencial de este algoritmo animó a muchos científicos a investigar las posibilidades de las computadoras cuánticas.
Uno de ellos fue el indio Lov Grover, quien estudió el problema de la búsqueda inversa: por ejemplo, dado un número de teléfono, buscar el nombre de usuario que le corresponde en el directorio telefónico. El problema directo —encontrar el número telefónico de un usuario— es muy fácil porque los nombres de los usuarios están en orden alfabético, pero la operación inversa requiere mucho más tiempo. Hay que buscar de uno en uno. En el peor de los casos, si por mala suerte el usuario que buscamos resulta ser el último de nuestra búsqueda, el proceso tomará tantos pasos como usuarios haya en el directorio. En 1996 Grover demostró que una computadora cuántica podría realizar esa búsqueda, y otras parecidas en una base de datos, en una cantidad de pasos igual a la raíz cuadrada del número de entradas en la base de datos. Esto es lo que hoy se conoce como algoritmo de Grover.
Un tercer ejemplo es el problema del viajante, que consiste en hallar el camino más corto que pase por n ciudades. La dificultad del problema crece de forma exponencial con el número de ciudades. Basta considerar 20 para que las combinaciones posibles se disparen a sesenta mil billones (un seis seguido de 16 ceros). Este es uno de los llamados problemas de optimización que tanta importancia tienen en la organización de muchas actividades, desde encontrar la ruta óptima para el reparto de mercancías hasta mejorar la eficiencia del transporte público. Una computadora cuántica podría reducir notablemente el tiempo necesario para encontrar la solución a este tipo de problemas.
Hacia la supremacía cuántica
Así pues, ¿qué esperamos para construir una computadora cuántica? El principal obstáculo es que las propiedades cuánticas que hacen especiales a los cúbits (superposición y entrelazamiento) son muy frágiles, y desaparecen ante la más mínima interacción con el entorno. Dicho de otro modo, si los cúbits no están perfectamente aislados, la más mínima perturbación introducirá errores en los cálculos y alterará el resultado. Este efecto aumenta a medida que intentamos juntar un mayor número de cúbits, pues más difícil resulta conservar las condiciones cuánticas. Hasta 2017, el número máximo de cúbits que habían conseguido unir los científicos era 17.
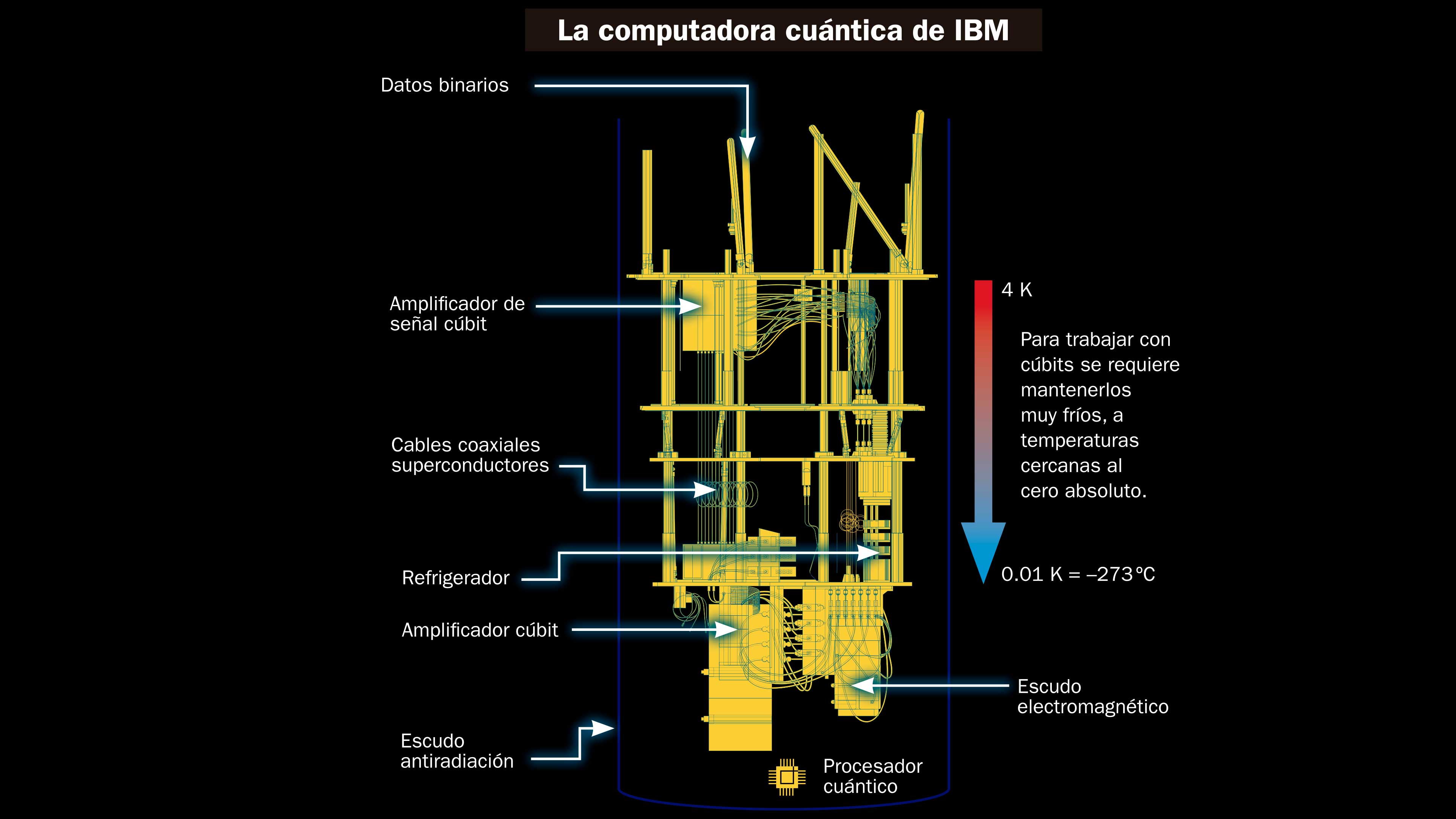
En la actualidad se conocen muy pocas maneras de construir un cúbit. La técnica más extendida utiliza corrientes en circuitos de superconductores (materiales que no oponen resistencia al paso de la corriente eléctrica cuando su temperatura baja de un cierto valor crítico). Con el fin de trabajar con estos cúbits el mayor tiempo posible es necesario mantenerlos muy fríos, a temperaturas cercanas al cero absoluto, inferiores a las del espacio exterior. A la vanguardia de esta nueva tecnología se encuentran grandes empresas como IBM y Google. Estos gigantes mundiales han sido noticia recientemente por dos hitos que nos acercan a las computadoras cuánticas comerciales.
El 18 de septiembre de ese mismo año, IBM publicaba la construcción de una computadora cuántica de 53 cúbits, casi el triple que su anterior computadora, que tenía 20. Al día siguiente, el 19 de septiembre, investigadores de Google anunciaban un logro histórico: la construcción de una computadora cuántica de 53 cúbits con la que habrían alcanzado la anhelada “supremacía cuántica” —es decir, resolver un problema que ninguna computadora clásica podría resolver en un plazo razonable—. El problema que atacó Google es comprobar que las cifras creadas por un generador de números aleatorios son verdaderamente aleatorias. Según los cálculos de Google, una supercomputadora tardaría 10 000 años en realizar los cálculos. La computadora cuántica de la compañía, llamada Sycamore, ejecuta el algoritmo en sólo 200 segundos.
 Cables superconductores coaxiales.
Cables superconductores coaxiales.
El futuro
La supremacía cuántica supone un avance fundamental para la computación cuántica. Aunque el problema resuelto no tiene ninguna utilidad, es la primera vez que una computadora cuántica logra superar a una clásica. Es de esperar que en el futuro las computadoras cuánticas puedan utilizarse con otros fines más prácticos. Las simulaciones de sistemas complejos, como el nacimiento de una galaxia o la evolución del clima en nuestro planeta, alcanzarían un nivel de detalle único. Nuestro conocimiento de física de partículas o física atómica mejoraría gracias a las simulaciones de fenómenos que obedecen las leyes de la física cuántica, como anticipó Richard Feynman. De hecho, una computadora cuántica que manejara 1 000 cúbits sería capaz de representar el estado de todo el Universo, lo que incluiría las posiciones y velocidades de las 1090 partículas que se calcula que contiene el Cosmos.
Pero la física no sería la única ciencia que se beneficiaría de las computadoras cuánticas. En química, la predicción de las propiedades de moléculas complejas podría mejorar el diseño de nuevos materiales para usarse en diversos campos como la energía o la salud. La biología, la ingeniería, la economía y la inteligencia artificial también se beneficiarían de la capacidad de cálculo de las computadoras cuánticas.
Para muchas de estas tareas específicas podrían bastar 100 cúbits, lo que no está mucho más allá de las computadoras de IBM y Google. Más lejos quedaría una computadora cuántica universal, capaz de resolver cualquier tarea, y que necesitaría al menos 500 cúbits. Es posible que haga falta para ello un gran salto tecnológico, similar al que supuso la invención del transistor para la computación clásica a finales de la década de 1940.
En realidad las computadoras cuánticas nunca desplazarán del todo a las clásicas. Nadie espera que una computadora cuántica sirva para consultar el correo electrónico o navegar por internet. A mediano plazo, sin embargo, es difícil predecir hasta qué punto serán capaces de cambiar el mundo que nos rodea. El futuro es esperanzador y seguro que nos depara muchas sorpresas.
Más información
- ¿Qué es la computación cuántica?, Descubriendo la Física: www.descubriendo.fisica.unlp.edu.ar
- Sáenz de Cabezón, Eduardo, Derivando, “¿Qué es y cómo funciona la computación cuántica?”: www.youtube. com/watch?v=YpYuBEzfRlM
- Santaolalla, Javier, Date un voltio, “¿Qué son los ordenadores cuánticos?”: www.youtube.com/ watch?v=035rUtCPKWU
Daniel Martín Reina es físico y colaborador habitual de ¿Cómo ves? Actualmente es miembro del grupo de Investigación de Instrumentación Electrónica y Aplicaciones de la Universidad de Sevilla, España. Escribe el blog de divulgación La aventura de la ciencia: http:// laaventuradelaciencia.blogspot.mx