Retos 306

De saltos por el tablero

Claudia Hernández García

Ilustración: Santiago Solís Montes de Oca

Todas las piezas del ajedrez se mueven en línea recta. Quizá la única que nos hace dudar de esta verdad es el caballo, porque no se mueve sobre la diagonal de un cuadrado, como la reina o el alfil, sino por un rectángulo de 3 × 2.

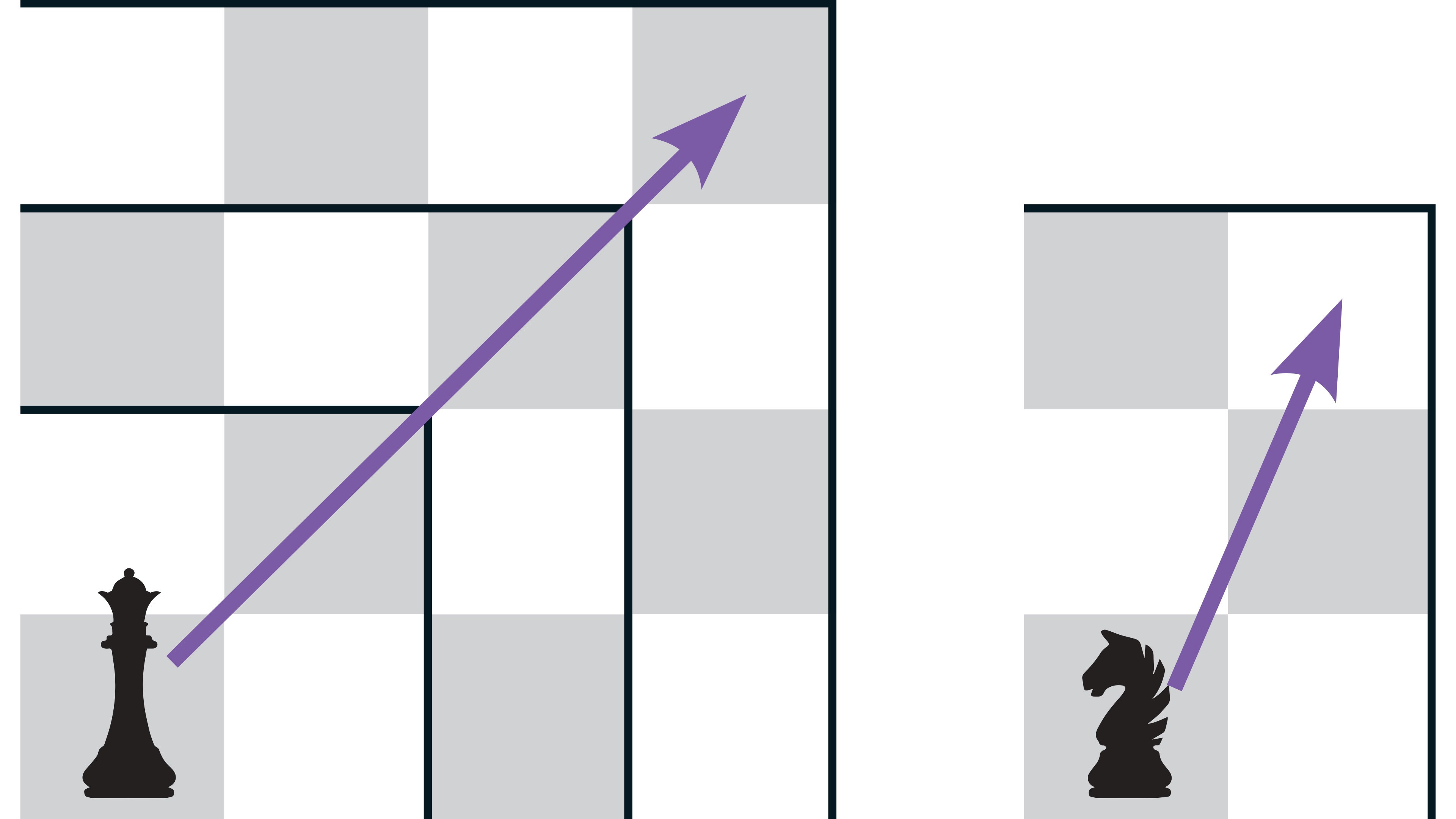
Tu propio teorema

Vamos a construir otra verdad sobre cómo se mueve esta pieza. Para ello hay que encontrar una regla que relacione el color del cuadrado de salida del caballo con el color del cuadrado de llegada, y luego hay que argumentar por qué, más o menos así: si el caballo sale de un cuadrado __________ siempre llegará a un cuadrado porque ___________. La pura enunciación de la regla es un ejemplo de lo que en matemáticas se conoce como conjetura. Cuando se argumenta sólidamente, entonces se convierte en teorema, y acabas de construir uno.

Dos soluciones

Lo que más asociamos con las matemáticas son los problemas. Uno típico del ajedrez es la pregunta de si es posible recorrer todo el tablero con los movimientos del caballo. Pues sí se puede, y aquí hay una solución que encontró Leonhard Euler en 1759 (a) y otra que publicó William Beverley en 1848 (b). El reto consiste en observar ambas soluciones y señalar dos propiedades de cada una.

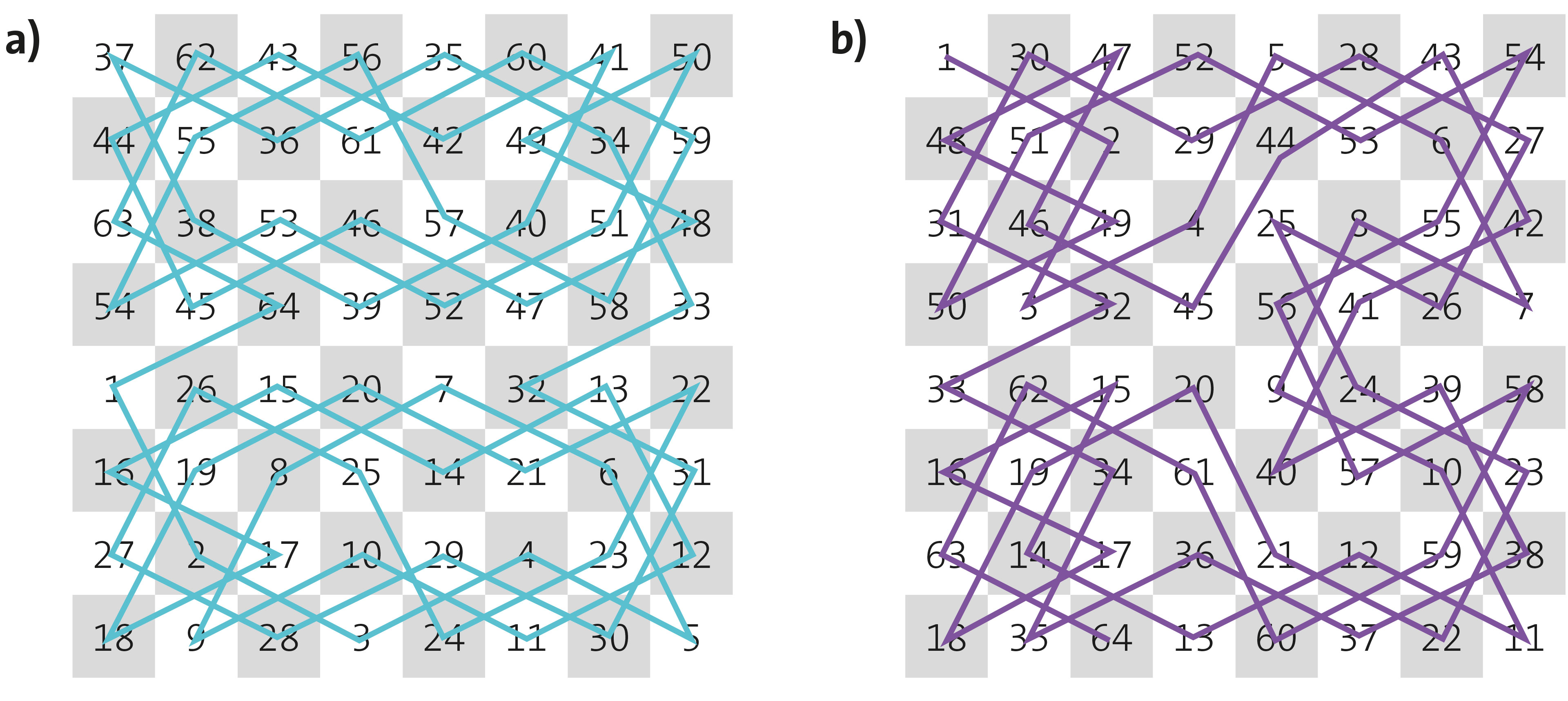
¿Necesitas una pista? Para a) fíjate en los números simétricamente opuestos con respecto al centro de la cuadrícula, como las casillas en contraesquina. Para b) fíjate en las filas y las columnas. Si hoy es de esos días en los que vienes con todo, puedes tratar de encontrar un recorrido propio.

Atacar a nadie

Otro típico desafío en el tablero de ajedrez es el de colocar cierta cantidad de piezas iguales sin que se ataquen. En la revista The American Mathe-matical Monthly de febrero de 1964 se publicaron argumentos que prueban que es posible colocar 32 caballos sin que se ataquen mutuamente. El reto consiste en hallar una manera de hacerlo. ¿No sabes por dónde empezar? Regresa al primer reto.