Retos 311
Seis lápices
Claudia Hernández García

Ilustración: Santiago Solís Montes de Oca
Un componente esencial para la resolución de los retos de esta sección es el pensamiento abstracto, un proceso cognitivo que nos lleva más allá de lo observable al mundo de las ideas, que es en donde generamos nuevas formas de pensar, conectamos conceptos que parecen no tener relación y esbozamos soluciones que no son obvias.
El pensamiento abstracto también nos ayuda a tener una comprensión más profunda de conceptos que pueden tener diferentes interpretaciones, además de que es crucial para la toma de decisiones, la innovación y la creatividad.
Vamos a ejercitar nuestro pensamiento abstracto con retos que requieren un material de lo más concreto: lápices, 6 para ser exactos. Los palillos también podrían servir, pero tienen que tener un poco de punta.
Sólo a uno
El primer reto consiste en colocar los 6 lápices sobre la mesa de manera que cada uno toque a otro lápiz y sólo a uno. O sea que no se vale que ningún lápiz toque a 2 o más. ¿Formaste un polígono al igual que yo? ¿Recuerdas cómo se llama?
Ahora sí, todos
El segundo reto consiste en volver a colocar los 6 lápices sobre la mesa, sólo que ahora cada uno debe tocar los otros 5. Si estás teniendo dificultad con este reto toma 3 lápices y forma una especie de abanico desde las puntas.
Cuatro triángulos
Este tercer reto nos obligará a salirnos de nuestra zona de confort: usemos nuestros 6 lápices para formar 4 triángulos. Obviamente no se vale cortarlos ni doblarlos.
2 x 1
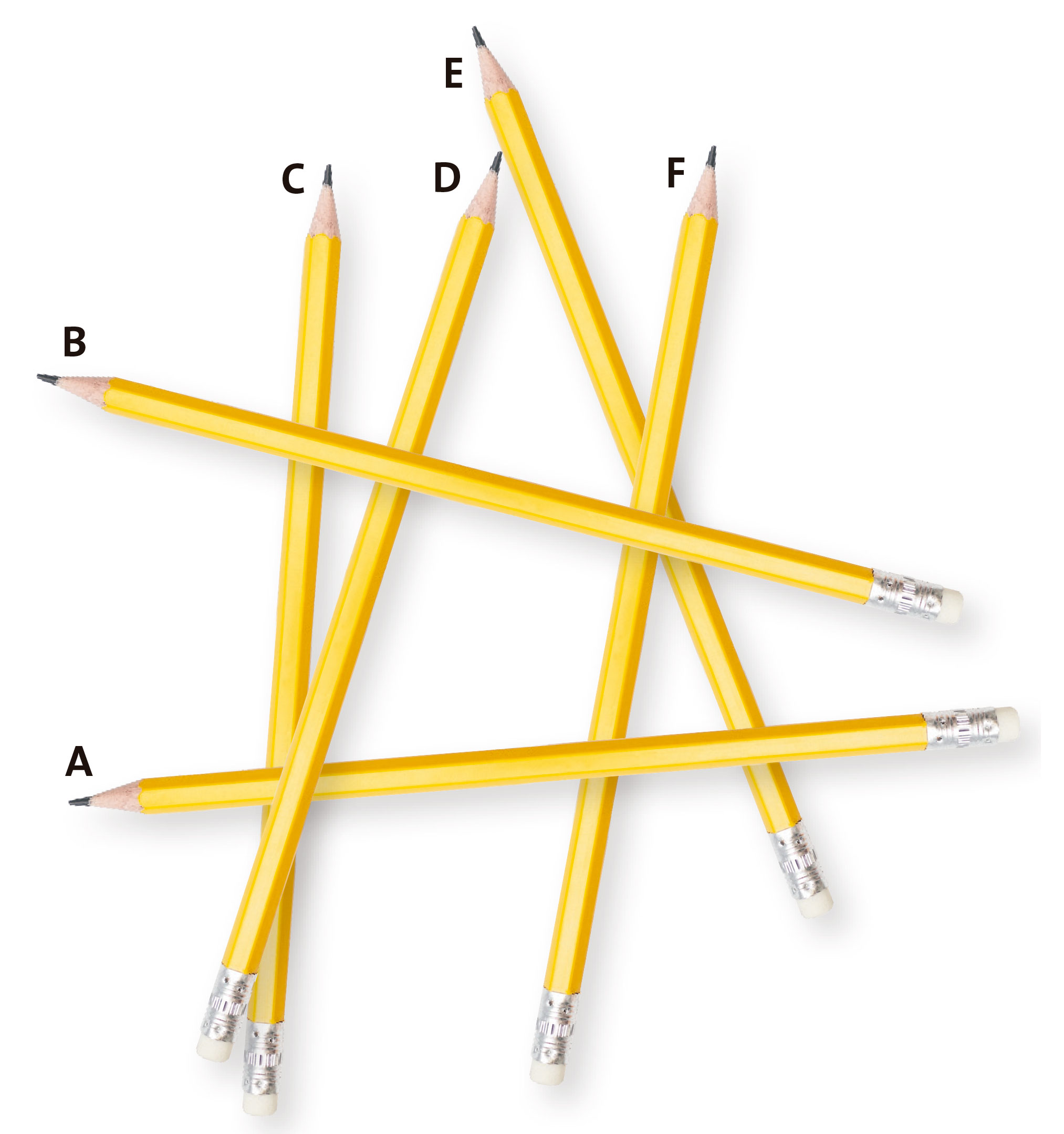
El último reto es doble. Fíjate en cómo están acomodados los lápices y elimínalos mentalmente. Sólo puedes quitar un lápiz si no tiene ninguno encima. Como bonus toma tus lápices y reproduce el montón de la imagen.
Soluciones núm. 310
Sumas de a dos. Aunque hay diez sumas posibles, sólo son siete resultados distintos: 4, 6, 8, 10, 12, 14 y 16. Si consideramos que los dígitos pueden sumarse consigo mismos, las dos respuestas adicionales son 2 y 18. Los números impares se escriben de la forma 2n + 1, o sea que cualquier número impar es resultado de sumar 1 al número par anterior. Al sumar dos números impares tenemos algo como esto: (2n + 1) + (2m + 1). Al reacomodar los sumandos tenemos 2n + 2m + 1 + 1 que es igual a 2n + 2m + 2, y esto también puede escribirse como 2(n + m + 1). Sin importar cuánto valen n y m, este número resultante será par porque es múltiplo de 2.
Sin repetir. Para encontrar la respuesta podemos descartar bloques completos de números que tienen nombres con letras repetidas: veintes, treintas, cuarentas, cincuentas, sesentas, setentas y noventas, así como los que contienen los números 5, 6, 7, 8 y 9. Al final sólo diez nombres de números no repiten letras: uno, dos, tres, cuatro, diez, once, doce, quince, ochenta y cien.
Mismo resultado. Dos números que cumplen la condición de escribirse como suma de dos cuadrados de dos maneras distintas son el 25 = 02 + 52 = 32 + 42 y el 50 = 12 + 72 = 52 + 52. ¿Ves cómo eso de sumar un número consigo mismo puede ser buena idea?















