Retos 315
Estrategia para contar
Claudia Hernández García

Ilustración: Santiago Solís Montes de Oca
Cuando contamos siempre tenemos que asegurarnos de dos cosas: de no contar ningún elemento más de una vez y de haberlos contado todos. Si no ponemos atención a esto no estamos haciendo un conteo sino un estimado. Para conseguir que estén todos los que son y sean todos los que están hay que pensar en una forma de organizar lo que vamos a contar y de marcar o separar lo que vamos contando para no repetir.
En orden y sin repetir
Como primer reto les propongo el siguiente ejercicio de conteo: ¿cuántos cuadrados hay en la siguiente imagen? En internet podrán encontrar la respuesta enseguida, pero me gustaría que se concentren en describir una estrategia que les asegure un conteo preciso y que la justifiquen.

Otros poquitos
Una característica esencial del pensamiento matemático es que una vez que encontramos una buena estrategia podemos extrapolarla a otro contexto, aunque a veces no funciona tal como la habíamos ideado o hay que considerar otras variables. El segundo reto consiste otra vez en contar los cuadrados que hay en la imagen, sólo que ésta tiene una pequeña variación que aumenta el nivel de dificultad.

Más allá de los cuadrados
En el tercer reto vamos a aumentar el nivel de dificultad: cambiaremos la forma geométrica que hay que buscar. Regresen a la primera cuadrícula y cuenten la cantidad de rectángulos que contiene.
Antes de empezar a contar los rectángulos traten de estimar si la cantidad será mayor, menor o igual que la que obtuvieron en el primer reto.
El pilón
Finalmente, les propongo hacer el conteo de una forma geométrica más compleja y en una estructura menos familiar. Ahora hay que encontrar la cantidad de heptágonos que hay en la siguiente imagen.
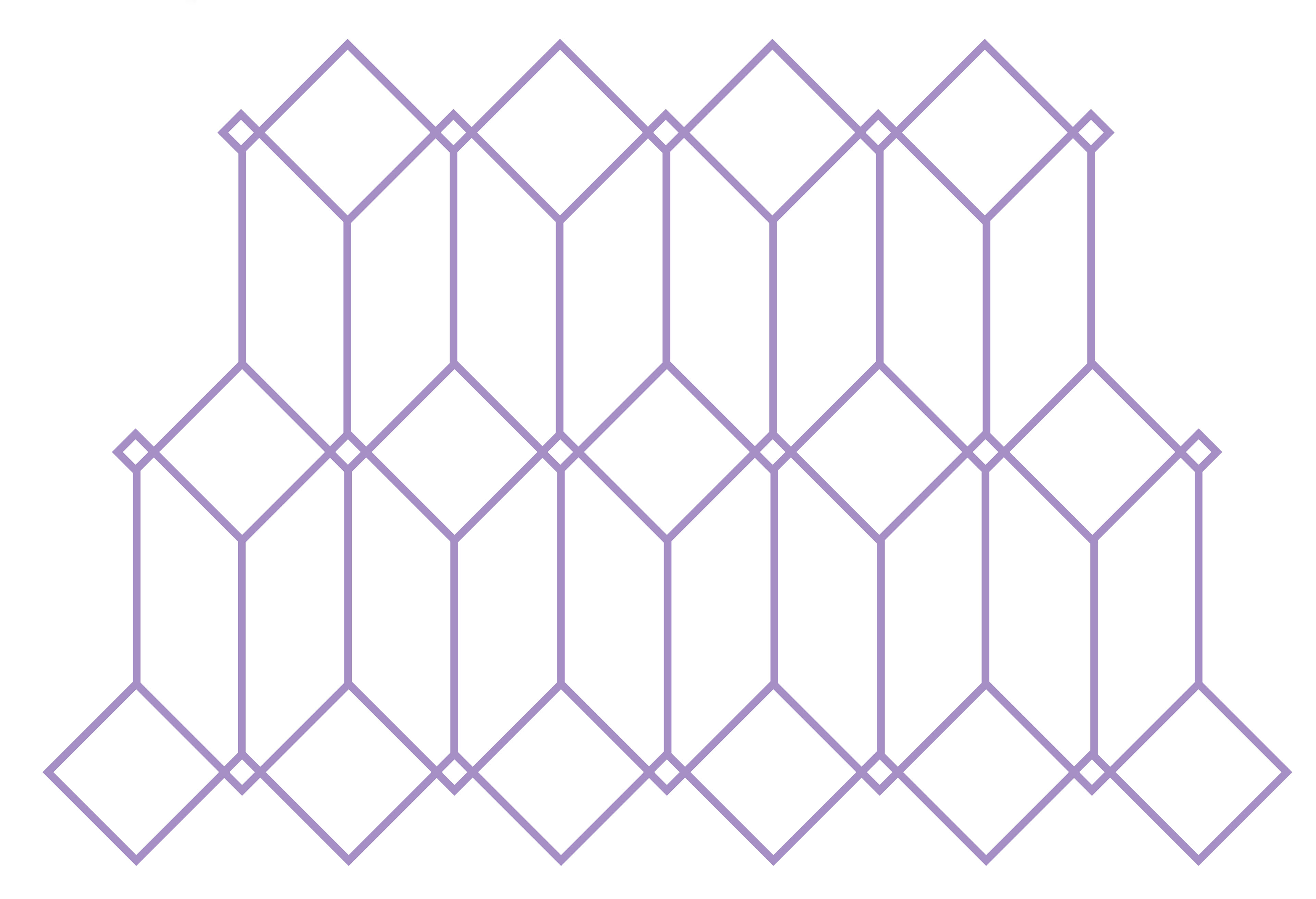
Si ya se cansaron de contar, nos vemos en los siguientes retos. Si todavía quieren seguirle, cuenten los cuadriláteros, los pentágonos, los hexágonos, los octágonos y los demás polígonos que encuentren.
Soluciones núm. 314
3+ resultados
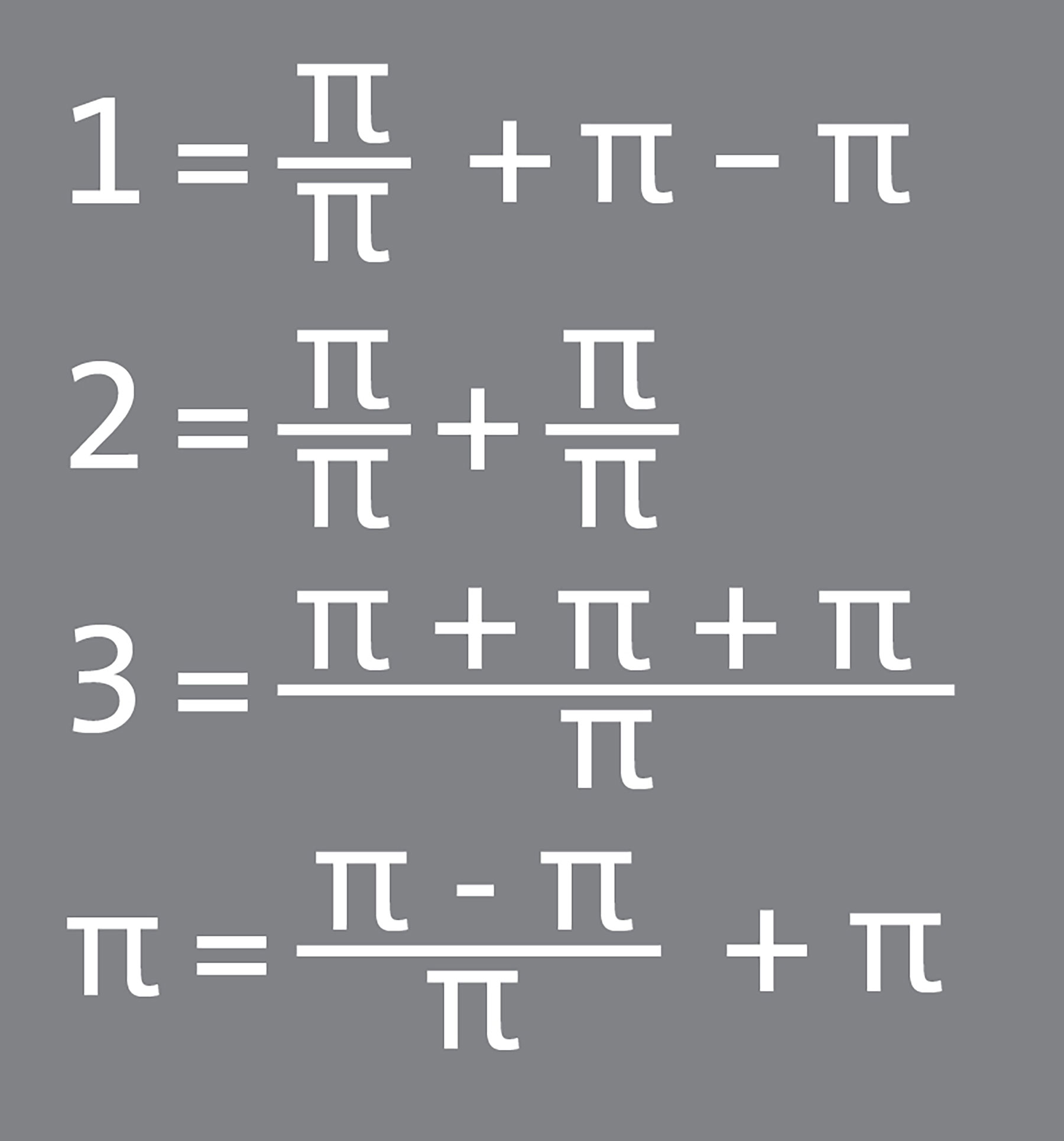
Fíjense que algo interesante de estas soluciones y de todos los retos como éste es que no importa con qué número trabajemos, siempre vamos a poder obtener los primeros números naturales de una forma más o menos similar.
Consecutivos y repetidos
Los primeros dos números consecutivos son 8 y 9 en la posición 11 y 12, respectivamente. El 3 se repite en los lugares 24 y 25, y el 1 se repite tres veces en la posición 51 a 53.















