Retos 319
Cuadrados mágicos
Claudia Hernández García

Ilustración: Santiago Solís Montes de Oca
Cuenta la leyenda que un día la furia divina provocó una tremenda inundación en China. Para apaciguarla la población hizo ofrendas al dios del río Luo, pero éste no las aceptó y en cambio envió una tortuga con unas peculiares marcas en el caparazón: una cuadrícula de 3 × 3 con arreglos de puntos acomodados de manera que las cantidades en cada columna, fila y diagonal sumaban lo mismo. Cuando los pobladores descifraron el misterio y presentaron dicha cantidad al dios las aguas volvieron a su cauce y pudieron confiar en que no habría más inundaciones.
Esta historia data del año 650 a.n.e., y por entonces a la cuadrícula se le atribuyó un significado místico. Lo que sabemos hoy es que esa configuración de puntos representa un cuadrado mágico que conocemos como Lo Shu.
Transformación
Los cuadrados mágicos son arreglos de números que cumplen la condición de que todas sus filas, columnas y diagonales suman lo mismo. A esa suma se le conoce como la constante mágica, y el orden del cuadrado es igual a la cantidad de filas o columnas que tiene. Por ejemplo, el cuadrado Lo Shu es de orden tres porque es de 3 × 3.
El primer reto consiste en elaborar el cuadrado mágico a partir de la información contenida en el caparazón de la tortuga y encontrar el valor de la constante mágica.
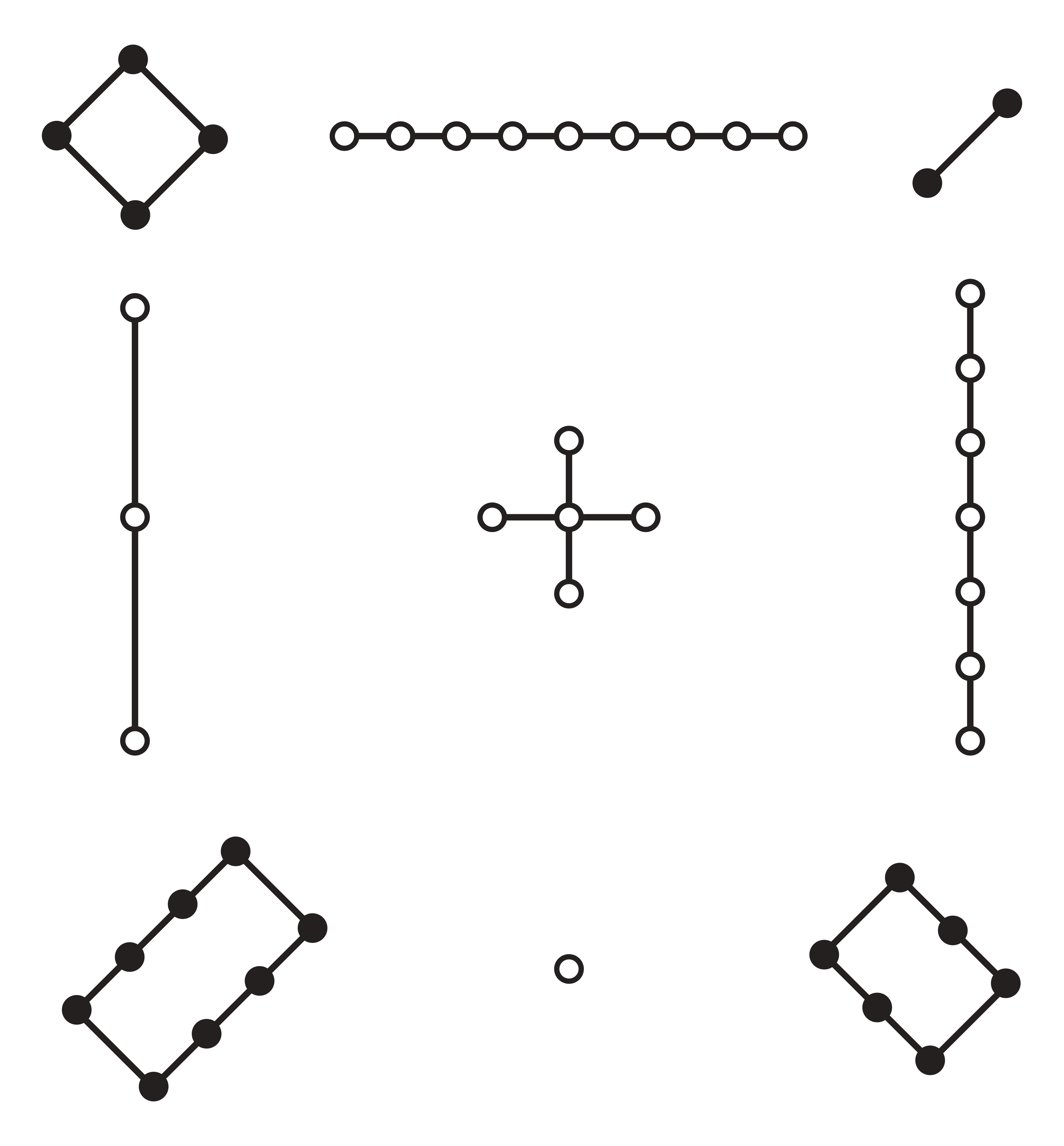
Si necesitas una pista comienza por contar los grupos de bolitas y acomódalos de acuerdo con su ubicación. Luego suma cualquier fila o columna y verás que da lo mismo: es un valor constante.
Otras soluciones
Existen otras formas de distribuir los dígitos del 1 al 9 en una cuadrícula de 3 × 3 que también resultan en cuadrados mágicos. El segundo reto es encontrar otras dos distribuciones distintas, una de forma libre y la otra siguiendo estas indicaciones.
- Escriban todas las tríadas de dígitos entre uno y nueve que sumen 15. ¿Cuántas diferentes obtuvieron? Ojo, 1 + 5 + 9 es equivalente a 1 + 9 + 5, a 5 + 9 + 1 y a todas las permutaciones posibles de esos tres dígitos.
- Ahora fíjense en cuántas veces aparece cada dígito en esa lista de sumas. ¿Cuál es el dígito que aparece menos veces y cuántas veces está? Averigüen lo mismo para el dígito que aparece más veces. ¿Hay algún dígito que aparezca una vez o cinco o más veces?
La misma, pero revuelta
Con eso tienen para obtener todas las configuraciones de cuadrados mágicos de orden tres, pero vamos a reforzar las ideas. El último reto consiste en encontrar patrones a partir de la información anterior con base en estas preguntas:
- ¿Cuál es el único dígito que puede ir en el lugar del punto naranja?
- ¿Cuáles dígitos pueden ir en donde están los puntos amarillos?
- ¿Cuáles pueden ir en lugar de los puntos rojos?

Quizá se pregunten si los cuadrados mágicos tienen alguna aplicación. La respuesta superficial es que no. Pero mientras resolvían los retos y contestaban las preguntas pusieron a prueba su capacidad de observación, encontraron patrones e hicieron generalizaciones, y todo en un nivel más profundo hizo que ejercitaran su mente. Así que la respuesta correcta es sí, resolver los cuadrados mágicos sí tiene sus beneficios.
Nos vemos el siguiente mes para más ejercicios mentales.
Soluciones núm. 318
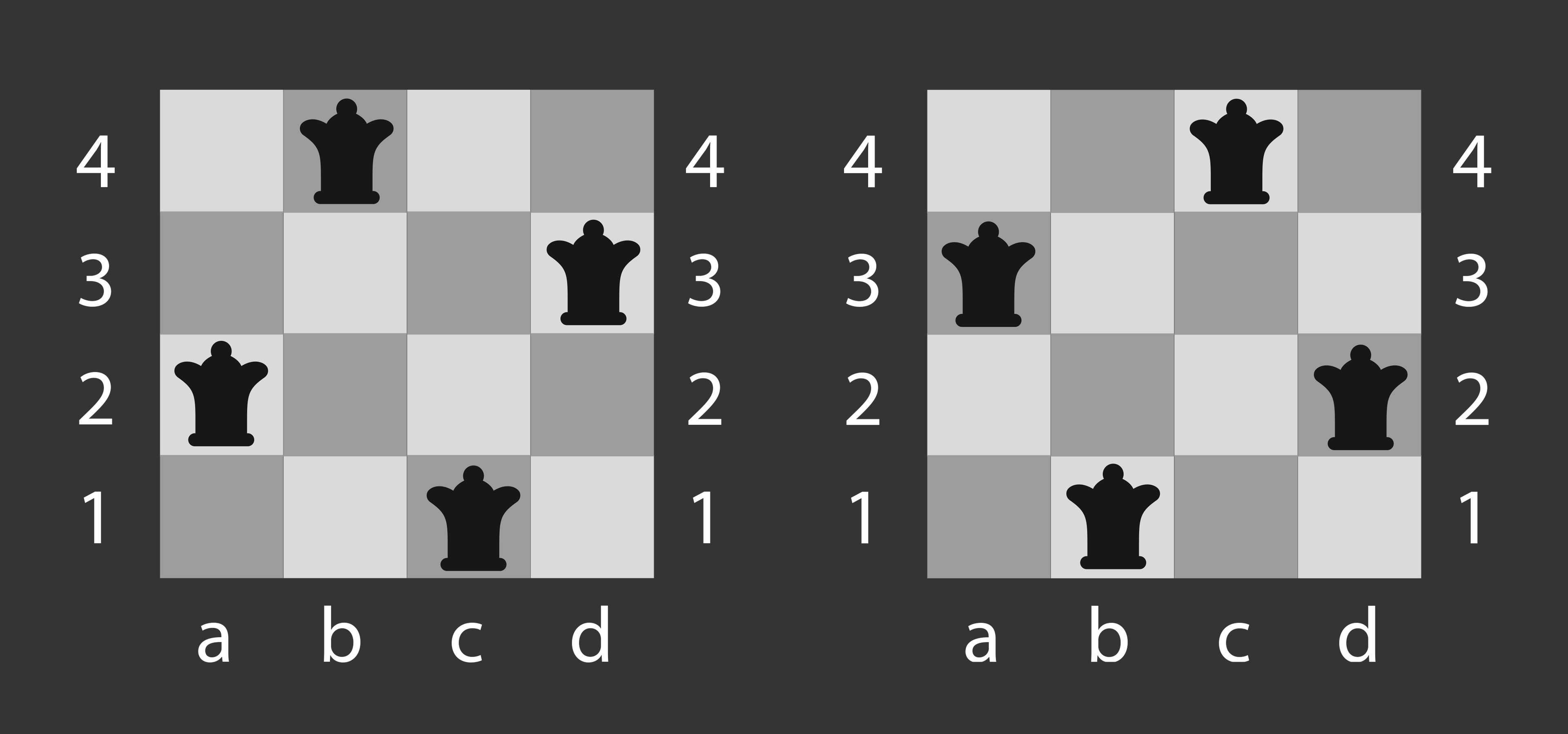
Tradicional con un giro. Todas las piezas se recorren una casilla en diagonal o una casilla a la derecha y luego una hacia arriba. Los casos más difíciles de ver son las reinas en h5 y en d8, por estar en la extrema derecha y hasta arriba, respectivamente. En el caso de la reina en h5, al moverla una casilla a la derecha la regresamos a a5 y al moverla una casilla hacia arriba llegamos a a6. La reina en d8 se mueve primero a e8 y finalmente regresa a e1.

Para completar. Esta solución no es equivalente a las presentadas en el primer reto.

Nivel anterior. Éstas son las dos soluciones. No son distintas porque una es reflejo de la otra.